Correlations and Variances
Question:
I need to compute correlations. How do I do that?
The script variance.jnl, included in the Ferret distribution, defines variables variance, correlation, and covariance based on the input variables. The variances are computed for each time series so if the input variables are defined in, say, X, Y, and time then the variance and correlations are functions of X and Y representing the correlation for each time series.
The variance script offers the following coaching lines about how to run it:
yes? go variance ... Variance and Covariance: Instructions: Use the LET/QUIET command to define the variable(s) P (and Q) as your variable(s) of interest (e.g. yes? LET/QUIET P = u[x=180,y=0]) The variance of P will be variable P_VAR (Q --> Q_VAR) The covariance will be COVAR The correlation will be CORREL. Type GO VAR_N to obtain n/n+1 statistical correction factor ...
Define variables P and Q as the inputs to the script (or to get a variance of only one variable, define P.) Both variables should have the same time axis. If they are on different grids, use a regridding transformation to regrid one variable in the time dimension to the grid of the other.
yes? SET DATA coads_climatology yes? LET p = sst[X=180,Y=10] yes? LET q = airt[X=180,Y=10] yes? GO variance
Here are our definitions of P and Q, and some of the variables that the script defines:
yes? SHOW VAR Created by DEFINE VARIABLE: >>> Definitions that replace any file variable of same name: P = SST[X=180,Y=10] Q = AIRT[X=180,Y=10] ... P_VAR = P_DSQ[L=@AVE] "VARIANCE OF P" Q_VAR = Q_DSQ[L=@AVE] "VARIANCE OF Q" P_VAR_MASK = P_DSQ_MASK[L=@AVE] "VARIANCE OF P WHEN Q PRESENT" Q_VAR_MASK = Q_DSQ_MASK[L=@AVE] "VARIANCE OF Q WHEN P PRESENT" COVAR = PQ_DSQ[L=@AVE] "COVARIANCE OF P AND Q" CORREL = COVAR / (P_VAR_MASK*Q_VAR_MASK)^.5 "CORRELATION OF P AND Q"
Listing the variances, correlation, and covariance,
yes? list p_var, q_var DATA SET: /home/ja9/tmap/fer_dsets/data/coads_climatology.cdf LONGITUDE: 179E LATITUDE: 9N TIME: 01-JAN 00:45 to 31-DEC 06:34 Column 1: P_VAR is VARIANCE OF P Column 2: Q_VAR is VARIANCE OF Q P_VAR Q_VAR I / *: 0.2455 0.1085 yes? LIST correl, covar DATA SET: /home/ja9/tmap/fer_dsets/data/coads_climatology.cdf LONGITUDE: 179E LATITUDE: 9N TIME: 01-JAN 00:45 to 31-DEC 06:34 Column 1: CORREL is CORRELATION OF P AND Q Column 2: COVAR is COVARIANCE OF P AND Q CORREL COVAR I / *: 0.6347 0.1036
The comments in variance.jnl suggest running var_n.jnl to make the n/n+1 correction. It is to be run after variance.jnl, and it redefines the variances to make that correction. So correlation and covariance are also redefined, as correl and covar are defined in terms of p_var and q_var.
Show the definitions of p_var and correl; see how p_var has a new definition after running the script var_n.jnl
yes? SHOW VAR p_var P_VAR = P_DSQ[L=@AVE] "VARIANCE OF P" yes? SHOW VAR correl CORREL = COVAR / (P_VAR_MASK*Q_VAR_MASK)^.5 "CORRELATION OF P AND Q" yes? GO var_n yes? SHOW VAR p_var P_VAR = P_DSQ[L=@AVE] * NDNM1 "VARIANCE OF P"
Note how correl has changed:
yes? LIST correl VARIABLE : CORRELATION OF P AND Q FILENAME : coads_climatology.cdf FILEPATH : /home/ja9/tmap/fer_dsets/data/ LONGITUDE: 179E LATITUDE : 9N TIME : 01-JAN 00:45 to 31-DEC 06:34 0.6347
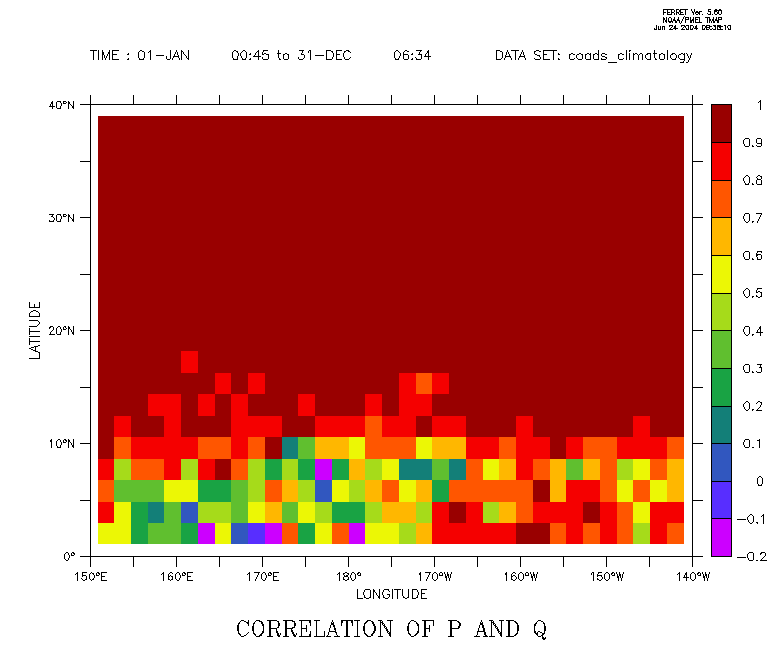
Now, if we want to define P and Q to be variables in X, Y, and time, we can see how the correlation varies in space, with higher correlations between sea and air temperature at latitudes where there is a stronger seasonal signal.
yes? SET DATA coads_climatology yes? LET p = sst[x=150:220,y=0:40] yes? LET q = airt[x=150:220,y=0:40] yes? go variance yes? go var_n
Note how correl is a function of X and Y
yes? STAT correl CORRELATION OF P AND Q LONGITUDE: 150E to 140W LATITUDE: 0 to 40N Z: N/A TIME: 01-JAN 00:45 to 31-DEC 06:34 DATA SET: /home/ja9/tmap/fer_dsets/data/coads_climatology.cdf Total # of data points: 700 (35*20*1*1) # flagged as bad data: 0 Minimum value: -0.18597 Maximum value: 0.9938 Mean value: 0.87395 (unweighted average) Standard deviation: 0.20548 yes? shade correl
See also the script correlation_with_students_t_test.jnl, new with Ferret v7.45. It calls the STUDENT_T_CUTOFF function and defines these additional variables :
- DEGREES_FREEDOM = degrees of freedom used available in calculating correlation, r.
- COVAR = covariance between input variables P and Q provided to variance.jnl
- CORREL = correlation, r.
- CORREL_SIGNIFICANT = correlation, r, for confidence level GE the specified percent probability cutoff.
- A variable named in the call to the script, defined to be = 1 or missing to denote that the correlation, r, is signficant (1) or not (missing).
yes? go/help correlation_with_students_t_test ...


