Every variable has an underlying grid which defines a coordinate space. All grids are in a sense 4 dimensional (X, Y, Z, and T) but axes normal to the data are represented as "normal" (such as the Z axis of the surface wind stress).
Grids can be viewed, specified and created using SHOW GRID, SET GRID, DEFINE AXIS, and DEFINE GRID. These commands are all in the Commands Reference section of this manual. Data can be regridded by the G= modifier. (See this chapter, section "Regridding")
Axes and grids can be explicitly created by DEFINE AXIS and DEFINE GRID. NetCDF and TMAP-formatted data set variables have all of the necessary grid and axis definitions embedded in the data set files, but if you are reading data from an ASCII or binary file, you must tell Ferret about the underlying grid of your data.
If you are creating abstract expressions entirely from pseudo-variables, you may want to define a grid in order to define the coordinate space of your calculation. This will also help produce a nicely labeled plot. (See the chapter "Variables and Expressions", "Grids and axes of pseudo-variables" and the example in the section on "Abstract Variables")
Example
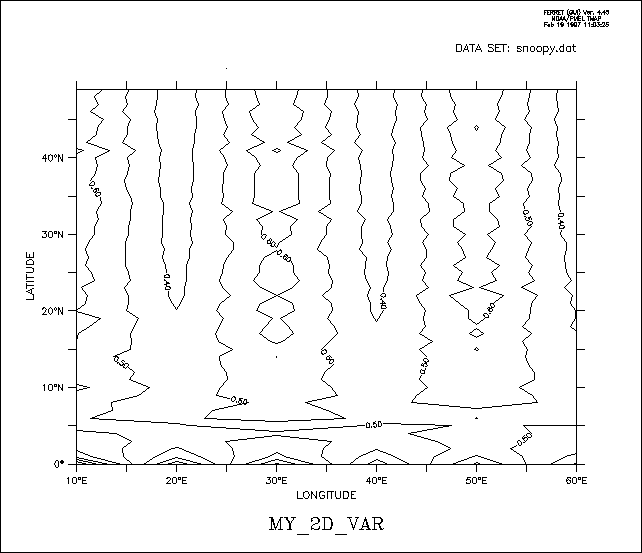
This example is taken from the demonstration script "file_reading_demo.jnl". An ASCII file contains a grid of numbers, 50 rows by 6 columns. Suppose the data are on a 2D grid of 6 longitudes by 50 latitudes (Figure 4_1).
yes? DEFINE AXIS/X=10E:60E:10/UNIT=DEGREE xlong yes? DEFINE AXIS/Y=0:49N:1/UNIT=DEGREE ylat yes? DEFINE GRID/X=xlong/Y=ylat gsnoopy2d ! By default only 1 column is read, /COLUMNS= specifies 6 columns yes? FILE/VAR=my_2D_var/COL=6/GRID=gsnoopy2d snoopy.dat yes? CONTOUR my_2D_var
4.2.2 Time axes and calendars
Data, particularly outputs from models, may be defined with time axes that are not on the standard Gregorian calendar. The netCDF conventions document discusses and defines usage for different calendars. These conventions for calendars are implemented in Ferret version 5.3 See:
NetCDF conforms to the conventions in the UDUNITS software package
www.unidata.ucar.edu/software/udunits/
The concept of time units and formatted time needs some thought and explanation. The possibility of using different calendar definitions also compilcates the question. Time coordinates (seconds, days, years, etc) are used by the software for computation and comparison. Formatted time (30-DEC-2003 00:00:00) is for the convenience of the human user.
Time coordinates, given as so many units (seconds, days, years, etc) since a reference time is generally impossible to comprehend at a glance. There has to be internal code to convert to formatted time. Conversion between the time-since-reference form and formatted time requires that we know the calendar. The calendar says how many days there are in each month, and hence also implies the length of the year, which therefore depends on the calendar.
The units second, minute, hour and day (24 hours) are always the same in all calendars we use for Earth and so the utilities can assume this. Models would expect to use these units when they write out times in timesteps.
Conversion to units of time (year month day hour minute second) is also needed when processing data to calculate means over months or other calendar-related intervals and climatological statistics. For computation, comparisons, plotting and regridding, Ferret makes the choice to adopt a common length of year for all calendars.
The default calendar in Ferret is the Gregorian calendar. This is implemented as a "proleptic" calendar, where the definition of a year is consistent throughout time and does not have an offset in the 1500's as the historical calendars did. However, files written using the NOAA/CDC standard for the "blended" Julian/Gregorian calendar are read correctly by Ferret: If a time axis has a time origin of 1-1-1 00:00:00, and uses the default calendar, and if the coordinates of axis lie entirely after the year 1582, then the historical 2-day shift is applied.
Other calendars may be defined using DEFINE AXIS/CALENDAR= or by reading a variable with a calendar attribute from a netCDF file. You can set the calendar type in a descriptor file, with the D_CALTYPE attribute.
Example:
$BACKGROUND_RECORD D_TITLE = 'Model Output, Daily Averages', D_T0TIME = '30-DEC-0000 00:00:00', D_TIME_UNIT = 3600., D_CALTYPE = 'NOLEAP', $END
The calendars that are defined for use in Ferret are
|
calendar name |
number of days/year |
notes |
|
GREGORIAN or STANDARD |
365.2425 |
default calendar (proleptic gregorian) |
|
JULIAN |
365.25 |
with leap years every 4 years |
|
NOLEAP or COMMON_YEAR |
365 |
no leap years |
|
ALL_LEAP or 366_DAY |
366 |
all years have 366 days |
|
360_DAY |
360 |
each month is 30 days |
If a time axis in a netCDF file has a calendar attribute with the value "PROLEPTIC_GREGORIAN" in a netCDF file, Ferret will treat it as having the standard calendar type. See the definition of the Proleptic Gregorian calendar, above.
Regridding between different calendars is allowed using the transformations @LIN (the default), @ASN, or @NRST. When regridding with @LIN from one calendar axis to another the length of a year is assumed to be constant, therefore the regridding calculates a scale factor based on the length of a second in each calendar, computed from the number of seconds per year for the calendars.
Example:
Define a calendar axis and regrid an existing variable to this axis:
yes? DEFINE AXIS/CALENDAR=JULIAN/T="15-JAN-1982":"15-DEC-1985":30/UNITS=days tmodel yes? LET twind = uwnd[GT=tmodel@NRST]
When using @MOD modulo regridding to compute a monthly climatology, the monthly climatology must be defined using the same calendar as the source data. See the section on modulo regridding for details.
The analysis of multi-year daily data is often awkward, because the length of the year changes for leap years. The analysis can often be made simpler by regridding the data to a NOLEAP calendar.
4.2.3 Dynamic grids and axes
The commands DEFINE AXIS and DEFINE GRID, described in the preceding section, should be used when the grid or axis will be referenced more than once and/or shared among several variables. In many cases it is more convenient to use dynamic (a.k.a. "implicit") grids and axes. Two quick examples:
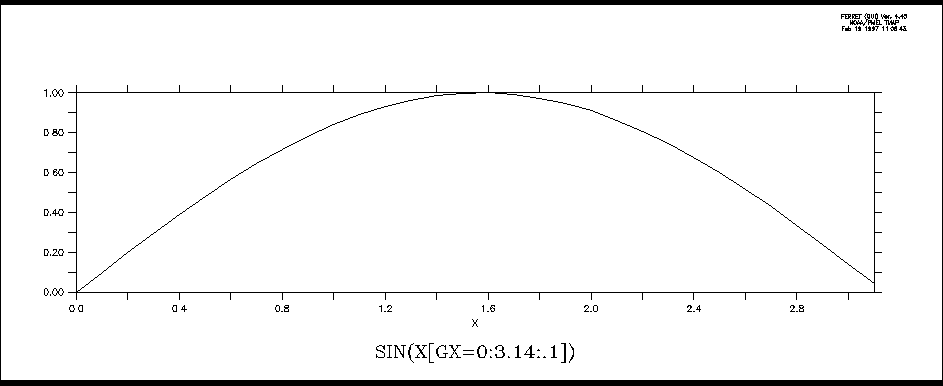
PLOT SIN(X[X=0:3.14:.1])
– dynamically creates an axis from 0 to 3.14 by 0.1
SHADE SST[X=140E:160W:5, D=coads_climatology]
– dynamically creates a longitude axis extending from 140E to 160W by 5 degrees, dynamically creates a grid which is like the grid upon which the variable SST is defined but with the X axis replaced by the new dynamic axis, and automatically regrids to this new grid.
4.2.3.1 Dynamic grids
It is often possible to avoid explicitly defining grids. This is useful in two common situations:
- Situation 1
Regridding to specified axes without the need for defining the destination grid.
Syntax: G*=name@transform, where
Example:
sst[GX=x10deg]
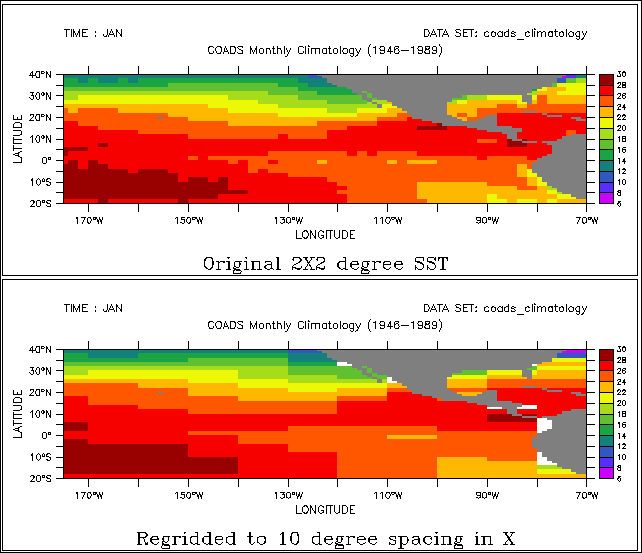
Suppose the variable SST is defined on a 2×2 degree grid in latitude/longitude (e.g., SET DATA coads_climatology). If we wish to regrid to 10-degree spacing in longitude over a range from 175W to 75W we could use the commands
DEFINE AXIS/X=175w:75w:10/UNITS=degrees x10deg LET sst10 = sst[GX=x10deg]
Several axes can be specified together when they are to be regridded similarly. For example, instead of sst[GX=x10deg, GY=y10deg] one can use the more concise sst[GXY=x10deg]
Similarly, av_sst[GZ=@AVE, GT=@AVE] can be condensed to av_sst[GZT=@AVE]
Ferret will dynamically create a grid equivalent to new_grid in
DEFINE GRID/LIKE=sst/X=x10deg new_grid.
Figure 4_2 shows the effects of regridding the 2×2 degree COADS data to a 10-degree spacing in longitude using (default) linear interpolation.
The command SHOW GRID SST10 will show the dynamically created grid. The names of dynamic grids and axes will always be displayed in parentheses.
Note that the transformation method to be used for regridding may also be specified, so LET SST10 = SST[GX=x10deg@ave] would create a 10-degree spaced result in which each grid point was computed as the weighted sum of the source points that fell within its grid box. The default method for regridding is linear interpolation.
• Situation 2
Automatic reconciliation of incompatible grid shapes
Syntax: G=name@transform
where
|
name |
– The name of a grid or of another variable defined on the desired grid |
|
@transform |
– The (optional) name of a regridding transform |
Example:
VAR1[g=VAR2]
If two variables are defined on grids that are mutually non-conformable because axes exist in one grid but do not exist (are NORMAL) in another, Ferret will now create a dynamic grid to resolve the non-conformabilities. This means that an expression of the form VAR1[G=VAR2] will be meaningful as long as the grid domains overlap.
For example, TEMP[d=levitus_climatology] is defined on an XYZ (time-independent) grid whereas SST[d=coads_climatology] is defined on an XYT grid. So to evaluate the expression SST[d=coads_climatology,G=TEMP[d=levitus_climatology]] Ferret will create a dynamic intermediate grid equivalent to
DEFINE GRID/LIKE=sst[D=coads_climatology]/X=temp/Y=temp
so that regridding occurs on the X and Y axes but the original grid structure is maintained with respect to depth and time.
The command SHOW GRID will reveal the resulting dynamically created grid structure.
4.2.3.2 Dynamic axes
The syntax "GX=lo:hi:delta" can be used in square brackets modifying a variable name to indicate the dynamic creation of an axis with the indicated range and spacing and the immediate regridding of the variable to a grid containing that axis. For example, SST[GX=175W:75W:10] will create a dynamic axis of 10-degree regular point spacing, will create a dynamic grid incorporating this axis (see previous section), and will regrid the variable SST to this grid.
Similarly, by referring to the grid indices rather than their world coordinates, the expression SST[GX=1:100:5] will create a dynamic axis that subsamples every 5th longitude point from SST. In this case the points of the resulting axis may be irregularly spaced if the points of the original axis were also irregular.
As with the dynamic regridding described above, transformations can be specified to indicate the regridding technique. Thus SST[GX=1:100:5@AVE] will use averaging instead of the default linear interpolation to perform the regridding.
As a notational convenience the "G" may be dropped when referring to dynamic axes. Thus SST[X=175W:75W:10] is equivalent to SST[GX=175W:75W:10] and SST[I=1:100:5@AVE] is equivalent to SST[GX=1:100:5@AVE]. When using this notational convenience keep in mind that a regridding is taking place, so the transformation applied (if any) must be a regridding transformation (see SHOW TRANSFORMS in the command reference).
The lower plot of Figure 4_2 illustrates the effect of dynamic axes in the command
SHADE SST[GX=175W:75W:10]
4.2.3.3 Dynamic pseudo-variables
The same notation used for dynamic axes may also be applied to pseudo-variables providing a simple means for creating arrays of values. For example, X[GX=0.2:1:0.2] is a vector of 5 points from 0.2 to 1 at a regular spacing of 0.2 units. The vector is oriented in the X direction.
An example of using such a vector is (Figure 4_3)
PLOT SIN(X[GX=0:3.14:.1])
Note that when the lo:high:delta notation is applied to T or L expressed as calendar dates the units of the delta value will be hours. For example, L[GT=1-jan-1980:1-feb-1980:24] is the integers 1 to 32 defined on an axis of 32 days, 24 hours apart.
As a notational convenience the "G" may be dropped when referring to dynamic pseudo-variables. Thus X[X=0.2:1:0.2] is equivalent to X[GX=0.2:1:0.2].
See also the discussion of pseudo-variables. and grids for pseudo-variables
4.2.4 Regridding
Syntax:
var[G=name] for (default) linear interpolation to new grid
or
var[G=name@trn] to regrid all axes using transform "trn" (see below)
or
var[G=name,GX=@TRN,GY=@TRN,...] to control regridding transformations along each axis separately
where
|
var |
is the name of the variable to be regridded (e.g., temp, u, tau, ...) |
|
name |
is the name of a variable (e.g., temp[G=u]) or the name of a grid (e.g., temp[G=gu01]) |
|
trn |
is the name of a special transformation (e.g., @AVE, @ASN, @LIN) |
The syntax var[G=name,GX=@TRN,GY=@TRN,...] can be compressed when specifying that several axes are to be regridded similarly. For example, instead of
var[GX=sst, GY=SST]
one can now use the more concise
var[GXY=sst]
Similarly, if using a regridding transformation,
var[GZ=@AVE, GT=@AVE]
can be condensed to
var[GZT=@AVE]
Note that in Ferret Version 5 and after when the limits of a variable are unspecified v2[g=v1] will default to the full extent of the v1 grid. Previously, it would become the size of whatever region of the v2 native grid overlapped with the v1 grid.
The Ferret distribution provides a demonstration of many regridding techniques:
yes? GO regridding_demo
Regridding is essential for algebraic operations that combine variables on incompatible grids. Ferret provides the commands DEFINE AXIS and DEFINE GRID to assist with the creation of arbitrary grids.
The result grid of a regridding operation does not necessarily match exactly the destination grid requested. For example, suppose the native grid of variable TEMP3D (Ocean Temperature) is 1 degree resolution in X and Y and 50 meter spacing in Z. If the syntax "[G=sst]" is used to request regridding to the grid of variable SST (Sea Surface Temperature), which is 2 degree resolution in X and Y, but normal to Z, then the resulting grid will be generated dynamically— inheriting X and Y axes from SST as requested, but retaining the Z axis of TEMP3D.
Examples
1) Suppose the variables u and temp are on staggered X, Y, and Z axes but share the same T axis. Then the two variables can be multiplied together on the axes (grid) of the u variable as follows:
yes? CONTOUR u * temp[G=u]
This will regrid temp onto the u grid by multi-axis linear interpolation before performing the multiplication.
2) Two variables, v1 and v2, are defined on distinct 4-dimensional grids (X, Y, Z, and T axes). The T axes of the two grids are identical but the X, Y, and Z axes all differ between the two variables. (This is often the case in numerical model outputs.)
To obtain the variable v1 on its original Z (depth) locations but regridded in the XY plane to the grid locations of the variable v2, define a new grid (say, named "new_grid") that has the X and Y axes of v2 but the Z axis of v1.
yes? DEFINE GRID/LIKE=v2/Z=v1 new_grid !define new grid yes? LIST/X=160E:140W/Y=5S:5N v1[G=new_grid] !request regridding
3) In this example we look at temperature data from two data sets. levitus_climatology, an annual climatology, has the variable "temp" on an XYZ grid which is 1×1 degree in XY, and coads_climatology, a monthly climatology, has the variable "sst" on an XYT grid which is 2×2 degrees in XY. Suppose we wish to look at the sea surface temperatures in January at the higher XY resolution of the Levitus data.
yes? SET DATA levitus_climatology yes? SET DATA coads_climatology yes? SET REGION/L=1/Z=0 yes? !get the name of the grid on which temp is defined yes? SHOW GRID temp[D=levitus_climatology] ! —> "Glevitr1" yes? DEFINE GRID/X=glevitr1/Y=glevitr1/Z=sst/L=sst glevitus_xy yes? LIST/X=150E:155E/Y=0:5N sst[G=glevitus_xy]
4) PyFerret/Ferret v7.6 includes support for Discrete Sampling Geometries (DSG) datasets, containing collections of Timeseries, Profiles, Trajectories, and Points. Regridding operations include regridding from a gridded dataset to the "grid" of a discrete data collection, which involves sampling the grid at the times and locations of the data.
yes? use reference_salinity_grid.nc yes? use dsg_profile_subset.nc yes? let salinity_on_profiles = salt[d=1, g=sal2[d=2]]
To regrid data from a discrete collection to a grid, use one of the SCAT2GRID functions. For details see the FAQ,
4.2.4.1 Regridding transformations
Ferret supports several regridding transformations. Use the SHOW TRANSFORMATIONS command to obtain a list of the supported transformations from Ferret. The choice of regridding transformation determines the computation by which data from the source grid determine the values on the destination grid.
Regridding transformations provide a means to perform a given calculation over a limited span of coordinates and repeat that calculation for a series of contiguous spans. For example, if we wish to compute the variance of the variable SST over 10-degree longitude range from 180 to 170W we could use the syntax sst[X=180:170w@VAR]. Now, if we wish to perform the same operation 10 times in 10-degree wide bands from 180 to 80W we could instead use G=@VAR regridding as in (see Dynamic Grids for an explanation of the "GX=" syntax):
DEFINE AXIS/X=175w:85w:10/UNITS=degrees ×10deg
LET sst10 = sst[GX=x10deg@VAR]
In addition to the regridding transformations here, see also Section 4.2.6, Auxiliary coordinate regridding, and particularly the Piecewise Linear averaging transformation, @PLAVE.
The regridding transformations are:
@LIN—linear interpolation (the default if no transform is specified)
Performs regridding by multi-axis linear interpolation between coordinate locations.
(Note that if there is just one point on the source or destination axis, a result is returned only if the coordinate locations match exactly.)
Computes the length-weighted average of all points on the source grid that lie partly or completely within each grid cell of the destination grid. If any portion of a source grid cell containing data overlaps a given destination grid cell, then data from that source cell contributes to the destination cell, weighted by the fraction of the destination cell overlapped by the source cell. The source data are treated as continuous, extending to the edges of the grid cells.
Note: When @AVE is applied simultaneously to the X and Y axes, where X and Y are longitude and latitude, respectively, an area-weighted average (weighted by cos(latitude)) is used. The @AVE transformation is unique in this respect. In multiple axis applications other than X and Y @AVE will be applied sequentially to the axes, computing the "average of the average." This may not be the desired weighting scheme in some cases. See @VAR below for an example.
Associates by subscript (blindly) the points from the source grid onto destination coordinates.
@BIN—unweighted mean; average by by binning
Computes the unweighted average of all valid data whose coordinate locations lie within each destination grid cell.
The number of valid data whose coordinate locations lie within each destination grid cell. This is an unweighted count. See @BIN.
Computes the variance of the points from the source grid that fall within each destination grid cell. This is a length-weighted computation like the @AVE transformation.
Note: This transformation is suitable for regridding only in a single axis. When applied simultaneously to two axes, for example, it will compute the variance of the variance. For example, V[gx=130E:80W:10@VAR, gy=205:20W:10@VAR] is equivalent to tmp[X=130E:80W:10@VAR] where tmp=V[y=20S:20N:10@VAR].
Compute the weighted number of points from the source grid that fall within each destination grid cell. Note that the results of this calculation need not be integers—this is a length-weighted computation like the @AVE transformation. It is common for a grid cell on the source grid to span the boundary between grid cells on the destination grid, thereby contributing a fraction of its weight to multiple destination grid cells. If the destination axis is the same as the source axis, then beginning with Ferret v7.42, the result is 1 for grid cells that have valid data and 0 otherwise. See also @NBIN
Note: This transformation is suitable only for regridding on a single axis. When applied simultaneously to two axes, for example, it will compute a constant. See @VAR for an example.
Nearest coordinate regridding VAR[GX=newaxis@NRST] chooses the value from the source axis coordinate closest to the destination axis. If source coordinates above and below are equally close to a destination coordinate the value at the lower coordinate will be chosen. (This is most useful for regridding between axes whose coordinate values are very close, though not exactly matched -- e.g. between equally and unequally spaced monthly time axes.)
Compute the indefinite integral. The integration is the weighted sum of the source variable from the start of the first cell specified on the source axis, to each coordinate value on the destination axis. When the destination axis for the regridding is the same as the source axis, the result is 0 at the bottom of the first grid cell, and is equal to the definite integral at the top of the uppermost grid cell. (The @IIN regridding transformation is new with Ferret v7.42).
Computes the length-weighted sum of the points from the source grid that fall within each destination grid cell. This is a length-weighted computation like the @AVE transformation.
Finds the minimum value of those points from the source grid that lie within each destination grid cell. Note that this is NOT a weighted calculation; the destination grid cell that "owns" a source point is determined entirely from the coordinate location of the source point, not from the limits of the source grid cell.
(As of Ferret V5.1) If a point on the source axis lies exactly on the boundary between grid cells on the destination axis it will be included in the calculations for the higher indexed cell on the destination axis. If a point on the source axis lies exactly on the upper cell boundary of the highest point on the destination axis, then it will be included in the calculations for that highest destination grid cell.
If you have data on a single point axis and you wish to embed it in a larger axis range you can achieve this by using either the G=@MIN or G=@MAX. For example,
yes? define axis/x=163e/npoints=1 x1pt yes? let var_1pt = randu(x[gx=x1pt]) ! a random value at a single coordinate yes? list var_1pt RANDU(X[GX=X1PT]) LONGITUDE: 163E 0.4914 yes? define axis/x=161e:165e:1 x5pt yes? list var_1pt[gx=x5pt@max] ! same value embedded within 5 point axis RANDU(X[GX=X1PT]) regrid: 1 deg on X@MAX 161E / 1: .... 162E / 2: .... 163E / 3: 0.4914 164E / 4: .... 165E / 5: ....
Finds the maximum value of those points from the source grid that lie within each destination grid cell. Note that this is NOT a weighted calculation; the destination grid cell that "owns" a source point is determined entirely from the coordinate location of the source point, not from the limits of the source grid cell..
(As of Ferret V5.1) If a point on the source axis lies exactly on the boundary between grid cells on the destination axis it will be included in the calculations for the higher indexed cell on the destination axis. If a point on the source axis lies exactly on the upper cell boundary of the highest point on the destination axis, then it will be included in the calculations for that highest destination grid cell.
The @MAX transformation is useful as a mechanism to perform regridding between two axes that do not quite match. A common example would be to regrid between two monthly axes one of which has points located at the 15th of each month and the other having points exactly at mid-month. These Ferret commands illustrate the example using a 5-month axis in 1993:
yes? DEFINE AXIS/UNIT=DAYS/T0=1-JAN-1900 month_15 = DAYS1900(1993,I[I1:5], 15) yes? DEFINE AXIS/UNIT=DAYS/T0=1-JAN-1900/EDGES month_mid = DAYS1900(1993,I[I=1:6], 1) yes? let my_var = L[gt=month_15 yes? list my_var L[GT=MONTH_15] 15-JAN-1993 00 / 1: 1.000 15-FEB-1993 00 / 2: 2.000 15-MAR-1993 00 / 3: 3.000 15-APR-1993 00 / 4: 4.000 15-MAY-1993 00 / 5: 5.000 yes? list my_var[gt=month_mid] L[GT=MONTH_15] regrid: on T 16-JAN-1993 12 / 1: 1.048 15-FEB-1993 00 / 2: 2.000 16-MAR-1993 12 / 3: 3.048 16-APR-1993 00 / 4: 4.033 16-MAY-1993 12 / 5: .... ! unable to interpolate yes? list my_var[gt=month_mid@max] L[GT=MONTH_15] regrid: on T@MAX 16-JAN-1993 12 / 1: 1.000 15-FEB-1993 00 / 2: 2.000 16-MAR-1993 12 / 3: 3.000 16-APR-1993 00 / 4: 4.000 16-MAY-1993 12 / 5: 5.000
Regridding with G=@XACT (or GX=@XACT, etc.) is a request to transfer values from a source grid to a destination grid only at those positions where there is an exact coordinate match between the source and destination axis points on the axis in question. Other destination points will be set to "missing". This transformation is especially useful for taking multiple in-situ data profiles, such as oceanographic cast data, and regridding them onto a regular (sparse) grid. For example: grep
yes? LET xcoarse = sin(x[x=0:20:10]) yes? LIST xcoarse SIN(X[X=0:20:10]) 0 / 1: 0.0000 10 / 2: -0.5440 20 / 3: 0.9129 yes? DEFINE AXIS/X=0:20:5 xfine yes? LIST xcoarse[gx=xfine@XACT] SIN(X[X=0:20:10]) regrid: 5 delta on X@XACT 0 / 1: 0.0000 5 / 2: .... 10 / 3: -0.5440 15 / 4: .... 20 / 5: 0.9129
@MOD
Creates climatologies from time series by regridding to a time series axis with a modulo regridding transformation. See the section on Modulo Regridding for details.
Examples
1) Let variable temp be defined on a grid with points spaced regularly at 1-degree intervals in both longitude and latitude (X and Y). Let grid "g10" possess points spaced regularly at 10-degree intervals in both X and Y.
yes? PLOT temp[G=g10] ! uses linear interpolation (@LIN) yes? PLOT temp[G=g10@AVE] ! area-averages 10x10 degrees of source\ points into each destination point. yes? PLOT temp[G=g10,GX=@AVE] ! averages 10 degrees of longitude but\ interpolates (@LIN) in Y.
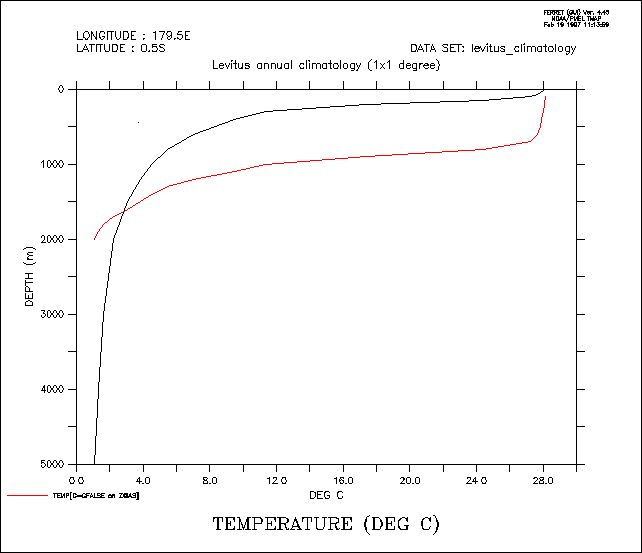
2) @ASN has the effect of bypassing Ferret's protections against misrepresenting data (Figure 4_4).
yes? SET DATA levitus_climatology yes? SET REGION/X=180/Y=0 ! true profile yes? PLOT/Z=0:5000 temp yes? DEFINE AXIS/DEPTH /Z=100:2000:100 zfalse yes? DEFINE GRID/LIKE=temp /Z=zfalse gfalse ! false profile yes? PLOT/Z=0:5000/OVER temp[G=gfalse@ASN]
4.2.5 Modulo regridding
Ferret can create climatologies from time series simply by regridding to a climatological axis with a modulo regridding transformation. For example, if the axis named month_reg is a 12-point monthly climatological (modulo) axis then the expression
LET sst_climatology = sst[D=coads,GT=month_reg@MOD]
is a 12-month climatology computed by averaging the full time domain of the input variable (576 points for coads) modulo fashion into the 12 points of the climatological axis.
Ferret has three pre-defined climatological axes: seasonal_reg (Feb, May, Aug, Nov), month_reg (middle of every month), and month_irreg (15th of every month). On opening Ferret or PyFerret these are defined:
> ferret
NOAA/PMEL TMAP
FERRET v7.4 (optimized)
Linux 2.6.32-696.18.7.el6.x86_64 64-bit - 04/27/18
24-May-18 09:54
yes? sh axis/all
name axis # pts start end
MONTH_IRREG TIME 12mi 16-JAN 12:00 15-DEC 17:49
MONTH_REG TIME 12mr 16-JAN 06:00 16-DEC 01:20
SEASONAL_REG TIME 4mr 15-FEB 15:43 15-NOV 14:05
MONTH_GREGORIAN TIME 12mi 16-JAN 12:00 15-DEC 17:49
MONTH_NOLEAP TIME 12mi 16-JAN 12:00 16-DEC 12:00
MONTH_360_DAY TIME 12mr 16-JAN 00:00 16-DEC 00:00
MONTH_ALL_LEAP TIME 12mi 16-JAN 12:00 16-DEC 12:00
MONTH_JULIAN TIME 12mi 16-JAN 12:00 15-DEC 18:00Datasets are available which define climatological axes for other calendars, Julian and noleap, and all possible seasonal calendars. To define these calendars, USE and CANCEL the axis-definition dataset. Datasets clim_axes_gregorian.nc, clim_axes_julian.nc, clim_axes_noleap.nc are distributed with Ferret beginning with the v7.4 release. They can be found at the GitHub Datasets page.
Note that MON_IRREG_GRG is the same as the pre-defined MONTH_IRREG and MON_REG_GRG is the same as MON_REG, included for naming consistency.
...
yes? USE clim_axes_gregorian
*** NOTE: regarding /home/users/tmap/ferret/linux/fer_dsets/data/clim_axes_gregorian.nc ...
*** NOTE: GREGORIAN climatological axes defined
yes? CANCEL DATA clim_axes_gregorian
yes? SHOW AXIS/ALL
name axis # pts start end
...
MON_IRREG_GRG TIME 12mi 16-JAN 12:00 16-DEC 17:49
JFM_IRREG_GRG TIME 4mi 15-FEB 02:54 16-NOV 05:49
DJF_IRREG_GRG TIME 4mi 15-JAN-0002 08:43 16-OCT-0002 23:38
NDJ_IRREG_GRG TIME 4mi 17-DEC 05:49 16-SEP-0002 11:38
MON_REG_GRG TIME 12mr 16-JAN 05:14 17-DEC 00:34
JFM_REG_GRG TIME 4mr 15-FEB 15:43 16-NOV 14:05
DJF_REG_GRG TIME 4mr 16-JAN-0002 11:03 17-OCT-0002 09:25
NDJ_REG_GRG TIME 4mr 17-DEC 00:34 16-SEP-0002 22:56
yes? use clim_axes_noleap
*** NOTE: regarding /home/users/tmap/ferret/linux/fer_dsets/data/clim_axes_noleap.nc ...
*** NOTE: NOLEAP climatological axes defined
yes? cancel data clim_axes_noleap
yes? show axis/all
...
MON_IRREG_NLP TIME 12mi 16-JAN 12:00 16-DEC 12:00
JFM_IRREG_NLP TIME 4mi 15-FEB 00:00 16-NOV 00:00
DJF_IRREG_NLP TIME 4mi 15-JAN-0002 00:00 16-OCT-0002 12:00
NDJ_IRREG_NLP TIME 4mi 17-DEC 00:00 16-SEP-0002 00:00
MON_REG_NLP TIME 12mr 16-JAN 05:00 16-DEC 19:00
In addition, there is an FAQ that describes how to create a daily climatological series, How do I compute a daily climatology for a time series? The analysis of multi-year daily data is often awkward, because the length of the year changes for leap years. The analysis can often be made simpler by regridding the data to a NOLEAP calendar.
!!!!! Prior to v6.9, need to USE and CANCEL this dataset. The next two !!!!! commands not nedded in v6.9 and higher yes? USE climatological_axes *** NOTE: regarding ... climatological_axes.cdf *** NOTE: Climatological axes SEASONAL_REG, MONTH_REG, MONTH_IRREG, TAX_GREGORIAN, TAX_NOLEAP, TAX_360_DAY defined yes? CANCEL DATA climatological_axes ! the axes are still defined
To generate a climatology based on a restricted range of input data simply define an intermediate variable with the desired points. For example, a monthly climatological time series based on data from the 1960s could be computed using
yes? LET sst_1960s = sst[D=coads,T=1-jan-1960:31-dec-1969] yes? PLOT sst_1960s[GT=month_reg@MOD]
If the source time axis uses a calendar other than the standard Gregorian calendar, then we need to use the appropriate climatological axis. The calendar can be found using the `var,RETURN=calendar` keyword.
yes? use my_surface_data yes? say `sst,return=calendar` !-> MESSAGE/CONTINUE NOLEAP NOLEAP
These calendars are pre-defined in Ferret: MONTH_IRREG, MONTH_REG, MONTH_GREGORIAN, MONTH_NOLEAP, MONTH_360_DAY, MONTH_ALL_LEAP, MONTH_JULIAN. MONTH_REG and MONTH_IRREG are defined on the default Gregorian calendar. MONTH_GREGORIAN is the same as MONTH_IRREG. Choose the monthly climatological axis with the same calendar as the source data:
yes? use my_surface_data yes? let sst_climatology = sst[GT=month_noleap@MOD]
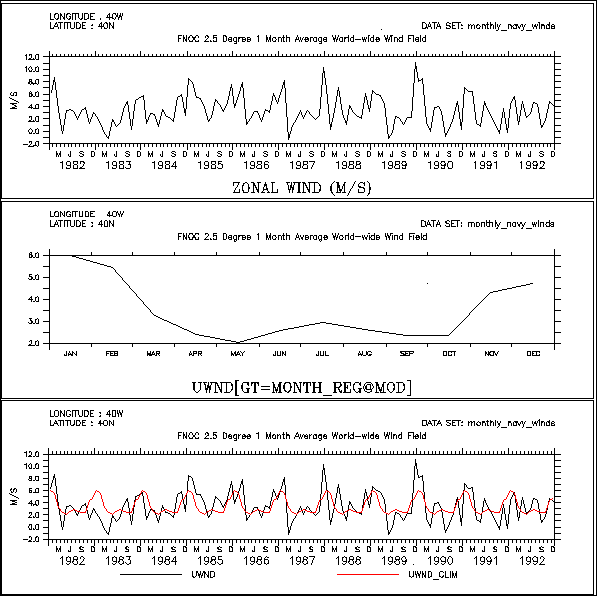
This example shows the entire sequence necessary to generate a plot of climatological SST at 40N, 40W based on the January 1982 to December 1992 Fleet Numerical wind data set. (Figure 4_5).
!!!!! Prior to v6.9, need to USE and CANCEL this dataset. The next two !!!!! commands not nedded in v6.9 and higher ! use the predefined climatological axes USE climatological_axes CANCEL DATA climatological_axes ! use the Fleet Numerical winds SET DATA monthly_navy_winds ! plot the raw data (top figure) SET REGION/X=40w/Y=40n plot uwnd ! plot the 12 month climatology (middle figure) LET uwnd_clim = uwnd[GT=month_reg@MOD] PLOT uwnd_clim ! since uwnd_clim is on a climatological axis ! Ferret can also plot it on the calendar axis with the raw data PLOT/T=16-jan-1982:17-dec-1992 uwnd,uwnd_clim
In many cases the volume of input data needed to perform climatological calculations is very large. In the example above the command
CONTOUR/X=0:360/Y=90s:90n sst_climatology[L=1]
to plot January from the climatology would require Nx*Ny*Nt=72*72*576=3 Megawords of data. Such calculations may be too large to fit into memory. However, if the region is fully specified (as shown for the X and Y limits in the example) Ferret's internal memory manager will break up the calculation as needed to produce the result. (See Memory Use in the chapter "Computing Environment", for further details.)
Unlike other transformations and regridding, modulo regridding is performed as an unweighted average: each non-missing source point contributes 100% of its weight to the destination grid box within which it falls. If the source and destination axes are not properly aligned this can lead to apparent shifts in the data. For example, if a monthly time series has data points at the first of each month and a climatological axis is defined at midmonths, then unweighted modulo averaging will lead to an apparent 1/2-month shift. To avoid situations of this type simply regrid to the climatological axis using linear interpolation prior to the modulo regridding.
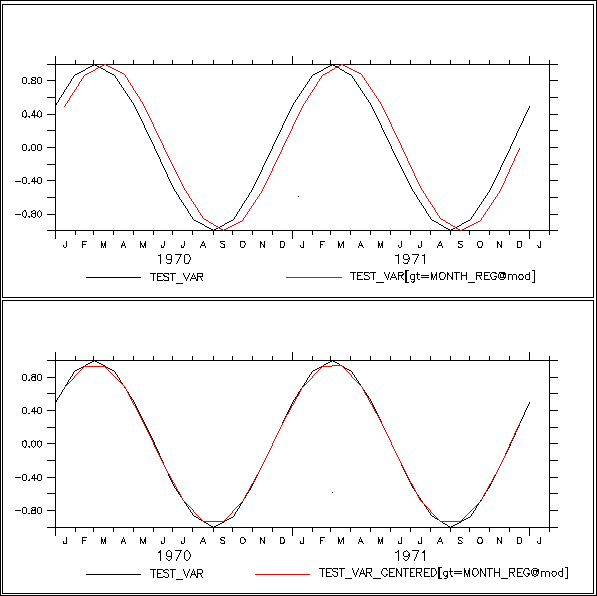
Here is an example that illustrates the situation and the use of linear interpolation to repair it. (Figure 4_6).
! define test_var, an illustrative variable with 1 year periodicity ! Note: test_var points are at the **beginnings** of months DEFINE AXIS/T=1-jan-1970:1-jan-1974:`365.25/12`/UNITS=days t10years DEFINE GRID/T=t10years gg LET test_var = SIN(L[G=gg]*2*3.14/12) ! plot 4 years of the cycle PLOT test_var ! define climatological axes at the midpoints of months !!!!! Prior to v6.9, need to USE and CANCEL this dataset. The next two !!!!! commands not nedded in v6.9 and higher USE climatological_axes CANCEL DATA climatological_axes ! notice that modulo regridding appears to shift the data ! (due to mis-aligned source and destination axes) (top figure) PLOT/OVER/T=1-jan-1970:1-jan-1974 test_var[GT=month_reg@MOD] ! to avoid the shift we can first regrid test_var to mid-month ! points using linear interpolation (the default regridding method) ! notice that the function test_var is largely unchanged by this LET test_var_centered = test_var[GT=month_reg] PLOT/OVER/T=1-jan-1970:1-jan-1974 test_var_centered ! finally perform a modulo regridding on well-aligned data ! notice that the shift is gone (bottom figure) PLOT/OVER/T=1-jan-1970:1-jan-1974 test_var_centered[GT=month_reg@MOD]
More notes:
In addition, modulo regridding can introduce biases if, say 2015 has 2 points lying in March and 2016 has 5 points in that same month. This is something to be aware of if the source data has many gaps.
Finally, please read the FAQ about computing climatologies and anomalies computing climatologies and anomalies. At the end are two notes about computing these with the best accuracy and lack of bias.
4.2.5.1 Modulo regridding statistics
In addition to the modulo averaging calculation performed by @MOD Ferret provides other statistics of the regridding. All modulo regridding calculations are unweighted as discussed under @MOD.
The variance of source points used to compute the result in each destination grid box: SUM((var-varbar)^2) / (n-1). That is, take each the source data value that goes into each modulo result-grid-cell. Subtract the modulo mean computed for its destination grid box, and square this difference. Divide by the number of points that went into each modulo-result grid box.
the sum of the source points within each destination grid box
the number of source points contributing to each destination grid box
the number of bad points in the region contributing to each destination grid box
the minimum value of the source points contributing to each destination grid box
the maximum value of the source points contributing to each destination grid box
Section 4.2.6. Using Auxiliary Coordinate Variables (logically rectangular grids)
Section 4.2.4 discusses how to regrid variables between rectilinear grids. A grid is rectilinear if each of its axes is rectilinear -- i.e. a simple, 1-dimensional sequence of points. On a rectilinear axis the relationship between real world coordinates and the corresponding indices is always one-to-one, for example depth=depth(k), lon=lon(i) and time-time(l). In this section we discuss how to work with ‘logically rectangular’ grids, a generalization of the concept of a rectilinear grid. Common examples of the logically rectangular (but non-rectilinear) grids that one may encounter include ‘layered vertical’ and ‘curvilinear horizontal’ coordinate systems. In a logically rectangular grid each real world coordinate (e.g. X, Y or Z) may depend upon multiple indices. For example, in a layered vertical coordinate system the Z real world coordinate (depth) typically depends upon the indices of the grid through depth=depth(i,j,k). In a curvilinear horizontal coordinate system each (lon, lat) position typically depends upon its index position through (lon(i,j), lat(i,j)), rather than the simpler rectilinear relationship of (lon(i), lat(j)).
In netCDF files that adhere to the Climate and Forecast (CF) conventions [http://cfconventions.org/] the attribute named coordinates is used to make associations between a scientific variable and the auxiliary coordinate variables upon which its grid depends. For example, if the scientific variable temp has a curvilinear horizontal coordinate system, then the netCDF file will contain the attribute
temp:coordinates=mylon, mylat;where mylon and mylat are two-dimensional variables that are also defined in the netCDF file, and share two dimensions of the variable temp. The netCDF-CF file “knows” that the shared dimensions represent the real world longitudes and latitudes, through the units attributes of the variables mylon and mylat, which would typically have values ”degrees_east” and ”degrees_north” respectively.
4.2.6.1 Regridding syntax for variables with auxiliary coordinates
Rectilinear regridding is invoked using the syntax
var[gW=axis@trans]
(See Section 4.2.4 of this Users Guide for general information about regridding syntax.)
The syntax to regrid a variable using auxiliary coordinate variables is an extension of the rectilinear regridding syntax:
var[gW(auxcoord)=axis@trans]
where
-
the regridding axis, W may be X, Y, Z, T, E, F. (also see shorthand syntax under Regridding from curvilinear horizontal coordinate systems below;
-
variable auxcoord is the auxiliary coordinate variable that defines W=W(indices);
-
the transformation algorithm used to perform the regridding is trans;
-
axis is the name of an axis; or a grid containing the desired axis in orientation W; or the name of a variable defined upon such a grid; or a triple of values given as lo:hi:delta, or (for linear interpolation, only) a single point value, or a pair of values defining a range over which transformation, trans, should be applied, such as lo:hi@PLAVE. The units of axis should match the units of auxcoord.
Auxcoord will typically be a variable that has been named as an auxiliary coordinate via a coordinates attribute in a netCDF dataset that follows the CF conventions. All of the axes that exist in the grid of auxcoord must also be found on the grid of the var. However, var may have axes not found on auxcoord (e.g. a time axis). The grid of auxcoord and the grid of var must share the Ferret axis in the W orientation.
For all single axes, regrid operations @trans may be @LIN (linear interpolation); or @PLAVE (average under the piecewise linear function implied by variable auxcoord over the bounds of each target grid cell -- see the Piecewise Linear averaging section of this document). The @LIN is the default when no transform is specified (see exception for FMRC time-forecast grids discussed below). If the target axis is a single numerical value, the @LINtransformation will always be used. Note that “@AVE” is also acceptable syntax to request averaging; it is interpreted as a synonym for “@PLAVE” (Piecewise Linear averaging)in the context of auxiliary coordinate regridding.
Regions: Auxiliary coordinate regridding treats region specifications in the same manner as traditional Ferret, namely region information always refers to the *target* grid. For example, in the command
SHADE/K=5:10 temp[gz(density)=myDensityAxis]
The K limits will be interpreted as indices of the axis myDensityAxis (versus the native Z axis of temp). (This behavior has serious implications for implementation, as discussed below.)
An example is shown in the FAQ, Density axis <--> depth axis.
4.2.6.2 Regridding from curvilinear horizontal coordinate systems
(not yet implemented as of 10/2015 -- syntax may change)
To regrid from a curvilinear to a rectilinear grid and to average over lat/long boxes
variants:
var[gxy(auxlon,auxlat)=grid_or_var@trans]
var[gx(auxlon)=xaxis@trans,gy(auxlat)=yaxis@trans]
var[gx(auxlon)=lo:hi:del@trans,gy(auxlat)=lo:hi:del@trans]
var[gx(auxlon)=xpt,gy(auxlat)=ypt]
The values of @trans for horizontal curvilinear regridding remain TBD at this time.
4.2.6.3 Auxiliary coordinate regridding using piecewise linear averaging
The following example illustrates the algorithm used when the requested regridding transform is piecewise linear averaging (@PLAVE) rather than linear interpolation. The conventional @AVE algorithm cannot be applied in this situation, because the functional relation between a variable (e.g. temperature) and its auxiliary coordinate (e.g. density) is only defined in terms of points, not grid cells, along the auxiliary coordinate.
Suppose the values shown just below represent a fragment of the variables density and temperature at some particular X,Y,T,E,F point as viewed on their native Z axis of depth (values are made-up for illustration)
depth density temp ... ... ... 10 1000.5 24.0 20 1001.5 23.5 50 1002.0 21.0 100 1003.5 19.0 ... ... ...
Suppose the requested regrid is
temp[gz(density)=1000:1004:2@PLAVE]
For any fixed X,Y,T,E,F grid point the averaging algorithm will regard temperature as a piecewise linear function of density. Consider as an example the target Z grid point at density=1002 -- a grid cell that extends from 1001 to 1003. The @PLAVE algorithm will find the average height of the temperature over this cell as the weighted average height of the 3 trapezoids shown in Figure 1. The grid cells of the target axis are indicated with the dark horizontal line; grid point locations marked with star symbols. This averaging algorithm contrasts with the typical (rectilinear axis) @AVE transformation (e.g. temp[Z=10:50@AVE]); @AVE regards each grid cell as having a constant value over the span of the cell (rectangles, rather than the trapezoids illustrated in Figure 4_8)
4.2.7 Forecast model Run Collections (FMRCs)
When a forecast model is run on an operational cycle, with a new model run commencing on a regular cycle, the resulting collection of multiple model outputs is called a Forecast model Run Collection (FMRC). An FMRC can be handled by Ferret as a single dataset, vastly reducing the effort needed to explore the data. The variables of each individual model run may include mixed 2D (surface) and 3D (volume) variables, mixed time-dependent and time-independent variables, and optionally an ensemble (E) 5th dimension. The individual model runs are assembled into a single dataset through the addition of a sixth “F” (forecast) start time axis. The new F axis is a calendar axis on which each coordinate point is the date/time at which that model run was commenced.
FMRCs are challenging to understand in detail, but quite easy to work with. A slide presentation providing both tutorial background and a sample session is available at
Using_Forecast_Model_Run_Collections_in_Ferret.pdf
The creation of the consolidated single dataset may be achieved using the Ferret DEFINE DATA/AGGREGATE/F command or using the THREDDS DATA SERVER (TDS) from Unidata. In either case, when the individual model runs are viewed in the context of the FMRC, the original time axes of the original model (which each differ) are replaced by a single uniform time axis in which each time step represents the elapsed time since the first time step of the model run. For example, if a forecast outputs snapshots 4 times daily, then the time axis of variables in that forecast run, when seen as part of the FMRC, will appear as a regular sequence 0, 6, 12, 18, … with units of hours. The true time steps of the individual model runs are preserved as a new variable that is synthesized by DEFINE/AGG/F (or by TDS). When created by the Ferret DEFINE DATA/AGGREGATE/F command the 2D time variable is named “TF_TIMES” (it will have a different name if the FMRC has been aggregated by TDS.) TF_TIMES is 2-dimensional variable, sharing the T and F axes of the other variables in the FMRC, where its value at each m,n index is the time step of that model snapshot as interpreted through the units of TF_TIMES. This time unit will follow the CF convention, e.g. “hours since 01-01-2015”.
The native form of the FMRC, as created by DEFINE AGGREGATION/F or TDS is the “compact” form of the FMRC. This form of the FMRC is efficient for storage and I/O, but is poorly suited (confusing) for analysis and visualization. There are two alternative representations of the variables in the FMRC that are better suited to these tasks. The most useful form is the ‘skill’ form, in which the T axis is a single long calendar axis that represents the date/time being modeled, and the F axis is the offset (lag) since the model run was initiated. The alternative form (less commonly used) is the ‘diagonal’ form. The slide presentation (see link above) clarifies these alternative forms.
Ferret’s auxiliary coordinate regridding syntax (Section 4.2.6.1) is used to transform the T and F axes of the compact form of an FMRC into the axes of the ‘skill’ and ‘diagonal’ forms. The 2-dimensional time coordinate variable, TF_TIMES (or other name if using TDS), must be provided as the auxcoord that guides the regridding. The ‘skill’ form of the FMRC is achieved by regridding both T and F
var[gt(tf_times)=TF_CAL_T,gf(tf_times)=TF_LAG_F]
The diagonal form of the FMRC may be achieved by regridding only the T axis
var[gt(tf_times)=TF_CAL_T@FMRC]
The explicit transformation “@FMRC” is required when regridding T only, to distinguish from the default linear interpolation transformation. When T and F regridding are requested together the “@FMRC” transformation is implicit, and therefore optional.
Starting in version 7.4.2, Ferret will, by default, find a common regular axis for the forecast initialization calendar times (TF_CAL_F) and the forecasted calender times (TF_CAL_T), and then define the elapsed time axes TF_LAG_T and TF_LAG_F in terms of this calendar axis. In order to find a common regular axis, some forecast initialization (calendar) times and some forecasted (calendar) times must match, and have a underlying regular axis. For instance, suppose every quarter-year (three months) one predicts conditions for every 1/12 of a year (month) of the next two years. (So every three months one has 24 new monthly predictions.) The common regular calendar axis will then be a monthly (1/12 of a year) axis starting at the time of the very first forecast and continuing to the end of the last forecasted time of the last forecast. (Currently, only this default behavior is available in FMRC aggregation; future versions for Ferret will allow specification of the calendar time axes as desired.)
The 2-dimensional time coordinate variable TF_TIMES is then defined using this common calendar axis. Because of this, forecasted values saved in the 'compact' form may first need to be regridded to the TF_LAG_T and TF_CAL_F axes before proceeding with the conversion to the 'diagonal' and 'skill' forms of the FMRC. For instance:
LET sparsevar = var[gt=TF_LAG_T@BIN,gf=TF_CAL_F@BIN] LET skillview = sparsevar[gt(tf_times)=TF_CAL_T,gf(tf_times)=TF_LAG_F]
The reason for this change is to properly represent the plots made, particularly the 'skill' plot. The regridding in the above example (using @BIN) puts in gaps between the forecasts in the 'compact' form, as there is a two-month gap between the start of each monthly forecast being made. When converted to the 'skill' plot, the proper gaps appear in the forecast lead time: on the month that a forecast is made, there is 'zero' forecast lead time. But on the months no forecast is made, there is no 'zero' forecast lead time but instead a one- or two-month forecast lead time. If one prefers the plots without these gaps, one could estimate the forecasts that would have been made in these off-months by interpolating (for example, using @LIN instead of @BIN) in the initial regridding of the 'compact' form.
A Ferret session plotting the above example forecast (two-year monthly forecasts made every quarter year) may look something like the following:
LET files = SPAWN("/bin/ls tmp/fcst_*.nc") DEFINE DATA /AGGREGATE /F /HIDE files SHADE /PALETTE=viridis /I=10 /J=10 fcst

LET sparse = fcst[gt=TF_LAG_T@BIN,gf=TF_CAL_F@BIN] SHADE /PALETTE=viridis /I=10 /J=10 sparse

LET diag = sparse[gt(TF_TIMES)=TF_CAL_T] SHADE /PALETTE=viridis /I=10 /J=10 diag

LET skill = sparse[gt(TF_TIMES)=TF_CAL_T,gf(TF_TIMES)=TF_LAG_F] SHADE /PALETTE=viridis /I=10 /J=10 skill

LET actual = skill[N=1] + 0.0 * _F LET error = skill - actual SHADE /PALETTE=red_blue_gray_centered /LEVEL=30CV /I=10 /J=10 error

This last plot assumes that the zero-lag forecasted values are actual conditions. Note that on months that a forecast was not made, actual conditions are not available. Again, one could produce plots without the gaps by estimating the actual conditions (and the missing forecasts) by interpolation.
See example plots in the section about defining FMRC datasets: DEFINE DATA/F