Throughout this manual, Ferret commands that require and manipulate data are informally called "action" commands. These commands are:
PLOT
CONTOUR
FILL (alias for CONTOUR/FILL)
SHADE
VECTOR
POLYGON
WIRE
LIST
STAT
LOAD
Action commands may use any valid algebraic expression involving constants, operators (+,–,*,...), functions (SIN, MIN, INT,...), pseudo-variables (X, TBOX, ...) and other variables.
A variable name may optionally be followed by square brackets containing region, transformation, data set, and regridding qualifiers. For example, "temp", "salt[D=2]", "u[G=temp"], "u[Z=0:200@AVE]", "v[k=1:50:5]
The expressions may also contain a syntax of:
IF condition THEN expression_1 ELSE expression_2
Examples: Expressions
i) temp ^ 2
temperature squared
ii) temp - temp[Z=@AVE]
for the range of Z in the current context, the temperature deviations from the vertical average
iii) COS(Y)
the cosine of the Y coordinate of the underlying grid (by default, the y-axis is implied by the other variables in the expression)
iv) IF (vwnd GT vwnd[D=monthly_navy_winds]) THEN vwnd ELSE 0
use the meridional velocity from the current data set wherever it exceeds the value in data set monthly_navy_winds, zero elsewhere.
+
–
*
/
^ (exponentiate)
AND
OR
GT
GE
LT
LE
EQ
NE
For instance the exponentiate operator can compute the square root of a variable as var^0.5
Ch3 Sec2.2. Multi-dimensional expressions
Operators and functions (discussed in the next section, Functions) may combine variables of like dimensions or differing dimensions.
If the variables are of like dimension then the result of the combination is of the same dimensionality as inputs. For example, suppose there are two time series that have data on the same time axis; the result of a combination will be a time series on the same time axis.
If the variables are of unlike dimensionality, then the following rules apply:
1) To combine variables together in an expression they must be "conformable" along each axis.
2) Two variables are conformable along an axis if the number of points along the axis is the same, or if one of the variables has only a single point along the axis (or, equivalently, is normal to the axis).
3) When a variable of size 1 (a single point) is combined with a variable of larger size, the variable of size 1 is "promoted" by replicating its value to the size of the other variable.
4) If variables are the same size but have different coordinates, they are conformable, but Ferret will issue a message that the coordinates on the axis are ambiguous. The result of the combination inherits the coordinates of the FIRST variable encountered that has more than a single point on the axis.
Examples:
Assume a region J=50/K=1/L=1 for examples 1 and 2. Further assume that variables v1 and v2 share the same x-axis.
1) yes? LET newv = v1[I=1:10] + v2[I=1:10] !same dimension (10)
2) yes? LET newv = v1[I=1:10] + v2[I=5] !newv has length of v1 (10)
3) We want to compare the salt values during the first half of the year with the values for the second half. Salt_diff will be placed on the time coordinates of the first variable—L=1:6. Ferret will issue a warning about ambiguous coordinates.
yes? LET salt_diff = salt[L=1:6] - salt[L=7:12]
4) In this example the variable zero will be promoted along each axis.
yes? LET zero = 0 * (i+j)
yes? LIST/I=1:5/J=1:5 zero !5X5 matrix of 0's
5) Here we calculate in-situ density; salt and temp are on the same grid. This expression is an XYZ volume of points (100×100×10) of density at 10 depths based on temperature and salinity values at the top layer (K=1).
yes? SET REGION/I=1:100/J=1:100
yes? LET t68 = 1.00024 * temp
yes? LET dens = rho_un (salt[K=1], t68[K=1], Z[G=temp,K=1:10])
Functions are utilized with standard mathematical notation in Ferret. The arguments to functions are constants, constant arrays, pseudo-variables, and variables, possibly with associated qualifiers in square brackets, and expressions. Thus, all of these are valid function references:
- EXP(-1)
- MAX(a,b)
- TAN(a/b)
- SIN(Y[g=my_sst])
- DAYS1900(1989,{3,6,9},1)
A few functions also take strings as arguments. String arguments must be enclosed in double quotes. For example, to test whether a dataset URL is available,
IF `TEST_OPENDAP("http://the_address/path/filename.nc") NE 0` THEN ...You can list function names and argument lists with:
yes? SHOW FUNCTIONS ! List all functions yes? SHOW FUNCTIONS *TAN ! List all functions containing string
Valid functions are described in the sections below and in Appendix A.
See also the section on string functions
It is generally advisable to include explicit limits when working with functions that replace axes. For example, consider the function SORTL(v). The expression
LIST/L=6:10 SORTL(v)
is not equivalent to
LIST SORTL(v[L=6:10])
The former will list the 6th through 10th sorted indices from the entire l range of variable v. The latter will list all of the indices that result from sorting v[l=6:10].
These functions in Ferret, including XSEQUENCE, SAMPLXY, and so on, are "grid-changing" functions. This means that the axes of the result may differ from the axes of the arguments. In the case of XSEQUENCE(sst), for example, the input grid for SST is
lon
lat
normal
time
whereas the output grid is
abstract
normal
normal
normal
so all axes of the input are replaced.
Grid-changing functions create a potential ambiguity about region specifications. Suppose that the result of XSEQUENCE(sst[L=1]) is a list of 50 points along the ABSTRACT X axis. Then it is natural that
LIST/I=10:20 XSEQUENCE(sst[L=1])
should give elements 10 through 20 taken from that list of 50 points (and it does.) However, one might think that "I=10:20" referred to a subset of the longitude axis of SST. Therein lies the ambiguity: one region was specified, but there are 2 axes to which the region might apply.
It gets a degree more complicated if the grid-changing function takes more than one argument. Since the input arguments need not be on identical grids, a result axis (X,Y,Z, or T) may be replaced with respect to one argument, but actually taken from another (consider ZAXREPLACE, for example.) Ferret resolves the ambiguities thusly:
If in the result of a grid-changing function, an axis (X, Y, Z, or T) has been replaced relative to some argument, then region information which applies to the result of the function on that axis will NOT be passed to that argument.
So, when you issue commands like
SET REGION/X=20E:30E/Y=0N:20N/L=1
LIST XSEQUENCE(sst)
the X axis region ("20E:30E") applies to the result ABSTRACT axis -- it is not passed along to the argument, SST. The Y axis region is, in fact, ignored altogether, since it is not relevant to the result of XSEQUENCE, and is not passed along to the argument.
The command SHOW FUNCTION/DETAILS lists the dependence of the result grid on the axes of the arguments:
yes? show func/details xsequence
XSEQUENCE(VAR)
unravel grid to a line in X
Axes of result:
X: ABSTRACT (result will occupy indices 1...N)
Y: NORMAL (no axis)
Z: NORMAL (no axis)
T: NORMAL (no axis)
E: NORMAL (no axis)
F: NORMAL (no axis)
VAR: (FLOAT)
Influence on output axes:
X: no influence (indicate argument limits with "[]")
Y: no influence (indicate argument limits with "[]")
Z: no influence (indicate argument limits with "[]")
T: no influence (indicate argument limits with "[]")
E: no influence (indicate argument limits with "[]")
F: no influence (indicate argument limits with "[]")Following is a partial list of Ferret Functions. More functions are documented in Chapter 7 (string functions), and in Appendix A.
MAX(A, B) Compares two fields and selects the point by point maximum.
MAX( temp[K=1], temp[K=2] ) returns the maximum temperature comparing the first 2 z-axis levels.
MIN(A, B) Compares two fields and selects the point by point minimum.
MIN( airt[L=10], airt[L=9] ) gives the minimum air temperature comparing two timesteps.
INT (X) Truncates values to integers.
INT( salt ) returns the integer portion of variable "salt" for all values in the current region.
ABS(X) absolute value.
ABS( U ) takes the absolute value of U for all points within the current region
EXP(X) exponential ex; argument is real.
EXP( X ) raises e to the power X for all points within the current region
LN(X) Natural logarithm logeX; argument is real.
LN( X ) takes the natural logarithm of X for all points within the current region
LOG(X) Common logarithm log10X; argument is real.
LOG( X ) takes the common logarithm of X for all points within the current region
SIN(THETA) Trigonometric sine; argument is in radians and is treated modulo 2*pi.
SIN( X ) computes the sine of X for all points within the current region.
COS(THETA ) Trigonometric cosine; argument is in radians and is treated modulo 2*pi.
COS( Y ) computes the cosine of Y for all points within the current region
TAN(THETA) Trigonometric tangent; argument is in radians and is treated modulo 2*pi.
TAN( theta ) computes the tangent of theta for all points within the current region
ASIN(X) Trigonometric arcsine (-pi/2,pi/2) of X in radians.The result will be flagged as missing if the absolute value of the argument is greater than 1; result is in radians.
ASIN( value ) computes the arcsine of "value" for all points within the current region
COS(X) Trigonometric arccosine (0,pi), in radians. The result will be flagged as missing of the absolute value of the argument greater than 1; result is in radians.
ACOS ( value ) computes the arccosine of "value" for all points within the current region
ATAN(X) Trigonometric arctangent (-pi/2,pi/2); result is in radians.
ATAN( value ) computes the arctangent of "value" for all points within the current region
ATAN2(Y,X) 2-argument trigonometric arctangent of Y/X (-pi,pi); discontinuous at Y=0.
ATAN2(Y,X ) computes the 2-argument arctangent of Y/X for all points within the current region.
MOD(A,B) Modulo operation ( arg1 – arg2*[arg1/arg2] ). Returns the remainder when the first argument is divided by the second.
MOD( X,2 ) computes the remainder of X/2 for all points within the current region
DAYS1900(year,month,day) computes the number of days since 1 Jan 1900, using the default Proleptic Gregorian calendar. This function is useful in converting dates to Julian days on the standard Gregorian calendar. If the year is prior to 1900 a negative number is returned. This means that it is possible to compute Julian days relative to, say, 1800 with the expression
LET jday1800 = DAYS1900 ( year, month, day) - DAYS1900( 1800,1,1)
MISSING(A,B) Replaces missing values in the first argument (multi-dimensional variable) with the second argument; the second argument may be any conformable variable.
MISSING( temp, -999 ) replaces missing values in temp with –999
MISSING( sst, temp[D=coads_climatology] ) replaces missing sst values with temperature from the COADS climatology
IGNORE0(VAR) Replaces zeros in a variable with the missing value flag for that variable.
IGNORE0( salt ) replaces zeros in salt with the missing value flag
Ch3 Sec2.3.19. RANDU and RANDU2
RANDU(A) Generates a grid of uniformly distributed [0,1] pseudo-random values. The first valid value in the field is used as the random number seed. Values that are flagged as bad remain flagged as bad in the random number field.
RANDU( temp[I=105:135,K=1:5] ) generates a field of uniformly distributed random values of the same size and shape as the field "temp[I=105:135,K=1:5]" using temp[I=105,k=1] as the pseudo-random number seed.
RANDU2(A, iseed) Generates a grid of uniformly distributed [0,1] pseudo-random values, using an alternate algorithm and allowing control over the random generator seed. Values that are flagged as bad remain flagged as bad in the random number field.
RANDU2( temp[I=105:135,K=1:5],iseed) generates a field of uniformly distributed random values of the same size and shape as the field "temp[I=105:135,K=1:5]" iseed is set as follows:
ISEED: -1=sys clock, 0=continue w/ previous seed, N>0 enter an integer value for a user-defined seed.
Ch3 Sec2.3.20. RANDN and RANDN2
RANDN(A) Generates a grid of normally distributed pseudo-random values. As above, but normally distributed rather than uniformly distributed.
A: field of random values will have shape of A
RANDN2(A, iseed) Generates a grid of normally distributed pseudo-random values. As above, but normally distributed rather than uniformly distributed.
A: field of random values will have shape of A
ISEED: -1=sys clock, 0=continue w/ previous seed, N>0 user-defined seed
RHO_UN(SALT, TEMP, P) Calculates the mass density rho (kg/m^3) of seawater from salinity SALT(salt, psu), temperature TEMP(deg C) and reference pressure P(dbar) using the 1980 UNESCO International Equation of State (IES80). Either in-situ or potential density may be computed depending upon whether the user supplies in-situ or potential temperature.
Note that to maintain accuracy, temperature must be converted to the IPTS-68 standard before applying these algorithms. For typical seawater values, the IPTS-68 and ITS-90 temperature scales are related by T_68 = 1.00024 T_90 (P. M. Saunders, 1990, WOCE Newsletter 10). The routine uses the high pressure equation of state from Millero et al. (1980) and the one-atmosphere equation of state from Millero and Poisson (1981) as reported in Gill (1982). The notation follows Millero et al. (1980) and Millero and Poisson (1981).
RHO_UN( salt, temp, P )
For example:
! Define input variables: let temp=2 ; let salt=35 ; let p=5000 ! Convert from IT90 to ITS68 temperature scale let t68 = 1.00024 * temp ! Define potential temperature ! at two reference pressure values let potemp0 = THETA_FO(salt, t68, P, 0.) let potemp2 = THETA_FO(salt, t68, P, 2000.) ! For sigma0 (sigma-theta, i.e., potential density) let rho0 = rho_un(salt, potemp0, 0.) let sigma0 = rho0 - 1000. ! For sigma2 let rho2 = rho_un(salt, potemp2, 2000.) let sigma2 = rho2 - 1000. ! For sigma-t (outdated method, sigma-theta is preferred) let rhot = rho_un(salt, t68, 0.) let sigmat = rhot - 1000. ! For sigma (in-situ density) let rho = rho_un(salt, t68, p) let sigma = rho - 1000.
THETA_FO(SALT, TEMP, P, REF) Calculates the potential temperature of a seawater parcel at a given salinity SALT(psu), temperature TEMP(deg. C) and pressure P(dbar), moved adiabatically to a reference pressure REF(dbar).
This calculation uses Bryden (1973) polynomial for adiabatic lapse rate and Runge-Kutta 4th order integration algorithm. References: Bryden, H., 1973, Deep-Sea Res., 20, 401–408; Fofonoff, N.M, 1977, Deep-Sea Res., 24, 489–491.
THETA_FO( salt, temp, P, P_reference )
NOTE: To do the reverse calculation, that is to convert from in-situ to potential temperature, we only need to inverse the 3rd and 4th arguments.
For example:
yes? LET Tpot = THETA_FO(35,20,5000,0)
yes? LET Tinsitu = THETA_FO(35,19,0,5000)
yes? LIST Tpot, Tinsitu
Column 1: TPOT is THETA_FO(35,20,5000,0)
Column 2: TINSITU is THETA_FO(35,19,0,5000)
TPOT TINSITU
I / *: 19.00 20.00
RESHAPE(A, B) The result of the RESHAPE function will be argument A "wrapped" on the grid of argument B. The limits given on argument 2 are used to specify subregions within the grid into which values should be reshaped.
RESHAPE(Tseries,MonthYear)
Two common uses of this function are to view multi-year time series data as a 2-dimensional field of 12-months vs. year and to map ABSTRACT axes onto real world coordinates. An example of the former is
yes? define axis/t=15-jan-1982:15-dec-1985/npoints=48/units=days tcal
yes? let my_time_series = sin(t[gt=tcal]/100)
yes? define axis/t=1982:1986:1 tyear
yes? define axis/z=1:12:1 zmonth
yes? let out_grid = z[gz=zmonth] + t[gt=tyear]
yes? let my_reshaped = reshape(my_time_series, out_grid)
yes? sh grid my_reshaped
GRID (G001)
name axis # pts start end
normal X
normal Y
ZMONTH Z 12 r 1 12
TYEAR T 5 r 1982 1986
For any axis X,Y,Z, or T if the axis differs between the input output grids, then limits placed upon the region of the axis in argument two (the output grid) can be used to restrict the geometry into which the RESHAPE is performed. Continuing with the preceding example:
! Now restrict the output region to obtain a 6 month by 8 year matrix
yes? list reshape(my_time_series, out_grid[k=1:6])
VARIABLE : RESHAPE(MY_TIME_SERIES, OUT_GRID[K=1:6])
SUBSET : 6 by 5 points (Z-T)
1 2 3 4 5 6
1 2 3 4 5 6
1982 / 1: 0.5144 0.7477 0.9123 0.9931 0.9827 0.8820
1983 / 2: 0.7003 0.4542 0.1665 -0.1366 -0.4271 -0.6783
1984 / 3: -0.8673 -0.9766 -0.9962 -0.9243 -0.7674 -0.5401
1985 / 4: -0.2632 0.0380 0.3356 0.6024 0.8138 0.9505
1986 / 5: 0.9999 0.9575 0.8270 0.6207 0.3573 0.0610
For any axis X,Y,Z, or T if the axis is the same in the input and output grids then the region from argument 1 will be preserved in the output. This implies that when the above technique is used on multi-dimensional input, only the axes which differ between the input and output grids are affected by the RESHAPE operation. However RESHAPE can only be applied if the reshape operation preserves the ordering of data on the axes in four dimensions. The RESHAPE function only "wraps" the variable to the new grid, keeping the data ordered as it exists in memory, that is, ordered by X (varying fastest) then -Y-Z-T (slowest index). It is an operation like @ASN regridding. Subsetting is done if requested by region specifiers, but the function does not reorder the data as it is put on the new axes. For instance, if your data is in Z and T:
yes? show grid my_reshaped
GRID (G001)
name axis # pts start end
normal X
normal Y
ZMONTH Z 12 r 1 12
TYEAR T 5 r 1982 1986
and you wish to put it on a new grid, GRIDYZ
yes? SHOW GRID gridyz
GRID (GRIDYZ)
name axis # pts start end
normal X
YAX LATITUDE 5 r 15N 19N
ZMONTH Z 12 r 1 12
normal T
then the RESHAPE function would NOT correctly wrap the data from G001 to GRIDYZ, because the data is ordered with its Z coordinates changing faster than its T coordinates, and on output the data would need to be reordered with the Y coordinates changing faster then the Z coordinates.
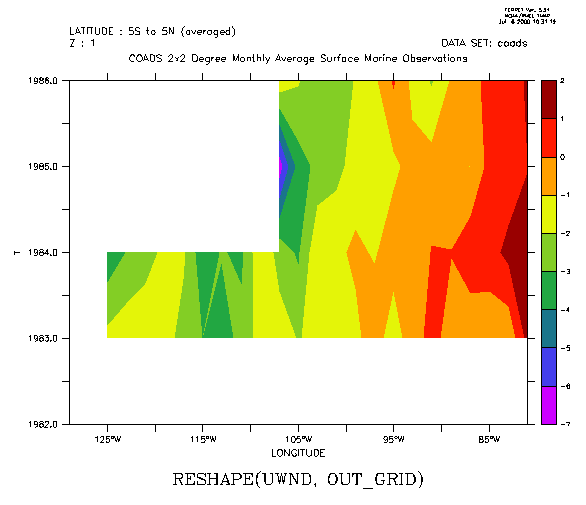
The following filled contour plot of longitude by year number illustrates the use of RESHAPE in multiple dimensions by expanding on the previous example: (Figure 3_2)
! The year-by-year progression January winds for a longitudinal patch ! averaged from 5s to 5n across the eastern Pacific Ocean. Note that ! k=1 specifies January, since the Z axis is month yes? USE coads yes? LET out_grid = Z[GZ=zmonth]+T[GT=tyear]+X[GX=uwnd]+Y[GY=uwnd] yes? LET uwnd_mnth_ty = RESHAPE(uwnd, out_grid) yes? FILL uwnd_mnth_ty[X=130W:80W,Y=5S:5N@AVE,K=1]
In the second usage mentioned, to map ABSTRACT axes onto real world coordinates, suppose xpts and ypts contain time series of length NT points representing longitude and latitude points along an oceanographic ship track and the variable global_sst contains global sea surface temperature data. Then the result of
LET sampled_sst = SAMPLEXY(global_sst, xpts, ypts)
will be a 1-dimensional grid: NT points along the XABSTRACT axis. The RESHAPE function can be used to remap this data to the original time axis using RESHAPE(sampled_sst, xpts)
yes? LET sampled_sst = SAMPLEXY(global_sst,\ ...? xpts[t=1-jan-1980:15-jan-1980],\ ...? ypts[t=1-jan-1980:15-jan-1980]) yes? LIST RESHAPE(sampled_sst, xpts[t=1-jan-1980:15-jan-1980])
When the input and output grids share any of the same axes, then the specified sub-region along those axes will be preserved in the RESHAPE operation. In the example "RESHAPE(myTseries,myMonthYearGrid)" this means that if myTseries and myMonthYearGrid were each multidimensional variables with the same latitude and longitude grids then
RESHAPE(myTseries[X=130E:80W,Y=5S:5N],myMonthYearGrid)
would map onto the X=130E:80W,Y=5S:5N sub-region of the grid of myMonthYearGrid. When the input and output axes differ the sub-region of the output that is utilized may be controlled by inserting explicit limit qualifiers on the second argument
ZAXREPLACE(V,ZVALS,ZAX) Convert between alternative monotonic Zaxes, where the mapping between the source and destination Z axes is a function of X,Y, and or T. The function regrids between the Z axes using linear interpolation between values of V. See also the related functions ZAXREPLACE_BIN and ZAXREPLACE_AVG which use binning and averaging to interpolate the values.
Typical applications in the field of oceanography include converting from a Z axis of layer number to a Z axis in units of depth (e.g., for sigma coordinate fields) and converting from a Z axes of depth to one of density (for a stably stratified fluid).
Argument 1, V, is the field of data values, say temperature on the "source" Z-axis, say, layer number. The second argument, ZVALS, contains values in units of the desired destination Z axis (ZAX) on the same Z axis as V — for example, depth values associated with each vertical layer. The third argument, ZAX, is any variable defined on the destination Z axis, often "Z[gz=zaxis_name]" is used.
The ZAXREPLACE function takes three arguments. The first argument, V, is the field of data values, say temperature or salinity. This variable is available on what we will refer to as the "source" Z-axis -- say in terms of layer number. The second argument, ZVALS, contains the values of the desired destination Z axis defined on the source Z axis -- for example, it may contain the depth values associated with each vertical layer. It should always share the Z axis from the first argument. The third argument, ZAX, is defined on the destination Z axis. Only the Z axis of this variable is relevant -- the values of the variable, itself, and its structure in X, Y, and T are ignored. Often "Z[gz=zaxis_name]" is used for the third argument.
Note:
ZAXREPLACE is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the arguments rather than a SET REGION command. See the discussion of grid-changing functions.
An example of the use of ZAXREPLACE for sigma coordinates is outlined in the FAQ on Using Sigma Coordinates.
Another example:
Contour salt as a function of density:
yes? set dat levitus_climatology ! Define density sigma, then density axis axden yes? let sigma=rho_un(salt,temp,0)-1000 yes? define axis/z=21:28:.05/depth axden ! Regrid to density yes? let saltonsigma= ZAXREPLACE( salt, sigma, z[gz=axden]) ! Make Pacific plot yes? fill/y=0/x=120e:75w saltonsigma
Note that one could regrid the variable in the third argument to the destination Z axis using whichever of the regridding transformations that is best for the analysis, e.g. z[gz=axdens@AVE]
Ch3 Sec2.3.25. XSEQUENCE, YSEQUENCE, ZSEQUENCE, TSEQUENCE, ESEQUENCE, FSEQUENCE
XSEQUENCE(A), YSEQUENCE(A), ZSEQUENCE(A), TSEQUENCE(A), ESEQUENCE(A), FSEQUENCE(A) Unravels the data from the argument into a 1-dimensional line of data on an ABSTRACT axis.
Note:
This family of functions are "grid-changing" functions; the output grid is different from the input arguments. Therefore it is best to use explicit limits on the argument rather than a SET REGION command. See the discussion of grid-changing functions.
FFTA(A) Computes Fast Fourier Transform amplitude spectra, normalized by 1/N
|
Arguments: |
A |
Variable with regular time axis. |
|
Result Axes: |
X |
Inherited from A |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
Generated by the function: frequency in cyc/(time units from A) |
See the demonstration script ef_fft_demo.jnl for an example using this function. Also see the external functions fft_re, fft_im, and fft_inverse for more options using FFT's
FFTA returns a(j) in
f(t) = S(j=1 to N/2)[a(j) cos(jwt + F(j))]
where [ ] means "integer part of", w=2 pi/T is the fundamental frequency, and T=N*Dt is the time span of the data input to FFTA. F is the phase (returned by FFTP, see next section)
The units of the returned time axis are "cycles/Dt" where Dt is the time unit of the input axis. The Nyquist frequency is yquist = 1./(2.*boxsize), and the frequency axis runs from freq1 = yquist/ float(nfreq) to freqn = yquist
Even and odd N's are allowed. N need not be a power of 2. FFTA and FFTP assume f(1)=f(N+1), and the user gives the routines the first N pts.
Specifying the context of the input variable explicitly e.g.
LIST FFTA(A[l=1:58])
will prevent any confusion about the region. See the note in chapter 3 above, on the context of variables passed to functions.
The code is based on the FFT routines in Swarztrauber's FFTPACK available at www.netlib.org. For further discussion of the FFTPACK code, please see the document, Notes on FFTPACK - A Package of Fast Fourier Transform Programs.
FFTP(A) Computes Fast Fourier Transform phase
|
Arguments: |
A |
Variable with regular time axis. |
|
Result Axes: |
X |
Inherited from A |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
Generated by the function: frequency in cyc/(time units from A) |
See the demonstration script ef_fft_demo.jnl for an example using this function.
FFTP returns F(j) in
f(t) = S(j=1 to N/2)[a(j) cos(jwt + F(j))]
where [ ] means "integer part of", w=2 pi/T is the fundamental frequency, and T=N*Dt is the time span of the data input to FFTA.
The units of the returned time axis are "cycles/Dt" where Dt is the time increment. The Nyquist frequency is yquist = 1./(2.*boxsize), and the frequency axis runs from freq1 = yquist/ float(nfreq) to freqn = yquist
Even and odd N's are allowed. Power of 2 not required. FFTA and FFTP assume f(1)=f(N+1), and the user gives the routines the first N pts.
Specifying the context of the input variable explicitly e.g.
LIST FFTP(A[l=1:58])
will prevent any confusion about the region. See the note in chapter 3 above, on the context of variables passed to functions.
The code is based on the FFT routines in Swarztrauber's FFTPACK available at www.netlib.org. See the section on Function FFTA for more discussion. For further discussion of the FFTPACK code, please see the document, Notes on FFTPACK - A Package of Fast Fourier Transform Programs .
SAMPLEI(TO_BE_SAMPLED,X_INDICES) samples a field at a list of X indices, which are a subset of its X axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
X_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
ABSTRACT; length same as X_INDICES |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common usage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions. For instance
yes? LET sampled_data = samplei(airt[X=160E:180E], xindices)
SAMPLEJ(TO_BE_SAMPLED,Y_INDICES) samples a field at a list of Y indices, which are a subset of its Y axis
|
Arguments: |
TO_BE_SAMPLED |
Data to be sample |
|
Y_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
ABSTRACT; length same as Y_INDICES |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common usage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLEK(TO_BE_SAMPLED, Z_INDICES) samples a field at a list of Z indices, which are a subset of its Z axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
Z_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
ABSTRACT; length same as Z_INDICES |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common usage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLEL(TO_BE_SAMPLED, T_INDICES) samples a field at a list of T indices, a subset of its T axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
T_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
ABSTRACT; length same as T_INDICES |
See the demonstration ef_sort_demo.jnl for a common usage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLEM(TO_BE_SAMPLED, E_INDICES) samples a field at a list of E indices, a subset of its E axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
E_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
|
|
E |
ABSTRACT; length same as E_INDICES |
|
|
F |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common usage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLEN(TO_BE_SAMPLED, F_INDICES) samples a field at a list of F indices, a subset of its F axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
F_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
|
|
E |
Inherited from TO_BE_SAMPLED |
|
|
F |
ABSTRACT; length same as F_INDICES |
See the demonstration ef_sort_demo.jnl for a common useage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLEIJ(DAT_TO_SAMPLE,XPTS,YPTS) Returns data sampled at a subset of its grid points, defined by (XPTS, YPTS)
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample, field of x, y, and perhaps z and t |
|
XPTS |
X coordinates of grid points to sample |
|
|
YPTS |
Y coordinates of grid points to sample |
|
|
Result Axes: |
X |
ABSTRACT, length of list (xpts,ypts) |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
This is a discrete version of SAMPLEXY. The points defined in arguments 2 and 3 are coordinaets, but a result is returned only if those arguments are a match with coordinates of the grid of the variable.
As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call. See the discussion of grid-changing functions.
SAMPLET_DATE (DAT_TO_SAMPLE, YR, MO, DAY, HR, MIN, SEC) Returns data sampled by interpolating to one or more times
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample, field of x, y, z and t |
|
YR |
Year(s), integer YYYY |
|
|
MO |
Month(s), integer month number MM |
|
|
DAY |
Day(s) of month, integer DD |
|
|
HR |
Hour(s) integer HH |
|
|
MIN |
Minute(s), integer MM |
|
|
SEC |
Second(s), integer SS |
|
|
Result Axes: |
X |
Inherited from DAT_TO_SAMPLE |
|
Y |
Inherited from DAT_TO_SAMPLE |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
ABSTRACT; length is # times sampled. The length is determined from the length of argument 2. |
As with other functions which change axes, specify any region information for the variable DAT_TO_SAMPLE explicitly in the function call. See the discussion of grid-changing functions.
Example:
List wind speed at a subset of points from the monthly navy winds data set. To choose times all in the single year 1985, we can define a variable year = constant + 0*month, the same length as month but with all 1985 data.
yes? use monthly_navy_winds
yes? set reg/x=131:139/y=29
yes? let month = {1,5,11}
yes? let day = {20,20,20}
yes? let year = 1985 + 0*month
yes? let zero = 0*month
yes? list samplet_date (uwnd, year, month, day, zero, zero, zero)
VARIABLE : SAMPLET_DATE (UWND, YEAR, MONTH, DAY, ZERO, ZERO, ZERO)
FILENAME : monthly_navy_winds.cdf
FILEPATH : /home/porter/tmap/ferret/linux/fer_dsets/data/
SUBSET : 5 by 3 points (LONGITUDE-T)
LATITUDE : 20N
130E 132.5E 135E 137.5E 140E
45 46 47 48 49
1 / 1: -7.563 -7.546 -7.572 -7.354 -6.743
2 / 2: -3.099 -3.256 -3.331 -3.577 -4.127
3 / 3: -7.717 -7.244 -6.644 -6.255 -6.099
SAMPLEXY(DAT_TO_SAMPLE,XPTS,YPTS) Returns data sampled at a set of (X,Y) points, using linear interpolation.
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample |
|
XPTS |
X values of sample points |
|
|
YPTS |
Y values of sample points |
|
|
Result Axes: |
X |
ABSTRACT; length same as XPTSand YPTS |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
Note:
SAMPLEXY is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the first argument rather than a a SET REGION command. See the discussion of grid-changing functions.
If the x axis represents longitude, then if the axis is marked as a modulo axis, the xpts will be translated into the longitude range of the the axis, and the sampled variable is returned at those locations.
Examples:
1) See the the script vertical_section.jnl to create a section along a line between two (lon,lat) locations; this script calls SAMPLEXY.
2) Use SAMPLEXY to extract a section of data taken along a slanted line in the Pacific.
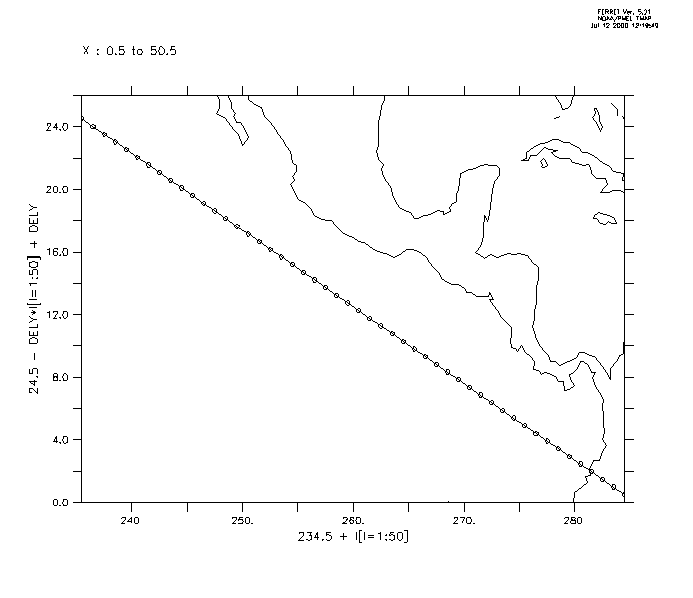
First we generate the locations xlon, ylat (Figure3_3a). One could use a ship track, specifying its coordinates as xlon, ylat.
yes? USE levitus_climatology ! define the slant line through (234.5,24.5) ! and with slope -24./49 yes? LET xlon = 234.5 + (I[I=1:50]-1) yes? LET slope = -1*24./49 yes? LET ylat = 24.5 + slope*(i[i=1:50] -1) yes? PLOT/VS/LINE/SYM=27 xlon,ylat ! line off Central America yes? GO land
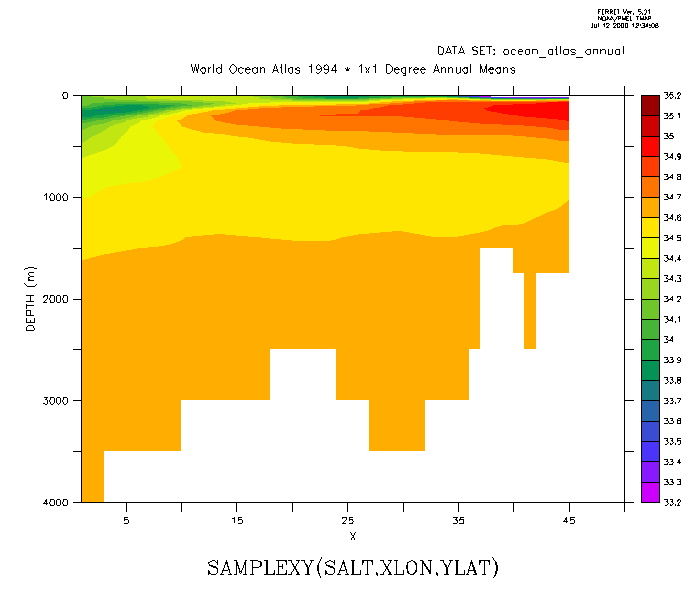
Now sample the field "salt" along this track and make a filled contour plot. The horizontal axis is abstract; it is a count of the number of points along the track. To speed the calculation, or if we otherwise want to restrict the region used on the variable salt, put that information in explicit limits on the first argument. (Figure3_3b)
yes? LET slantsalt = samplexy(salt[x=200:300,y=0:30],xlon,ylat) yes? FILL/LEVELS=(33.2,35.2,0.1)/VLIMITS=0:4000 slantsalt
Ch3 Sec2.3.35. SAMPLEXY_CLOSEST
SAMPLEXY_CLOSEST(DAT_TO_SAMPLE,XPTS,YPTS) Returns data sampled at a set of (X,Y) points without interpolation, using nearest grid intersection.
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample |
|
XPTS |
X values of sample points |
|
|
YPTS |
Y values of sample points |
|
|
Result Axes: |
X |
ABSTRACT; length same as XPTSand YPTS |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
Note:SAMPLEXY_CLOSEST is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the first argument rather than a SET REGION command. See the discussion of grid-changing functions.
This function is a quick-and-dirty substitute for the SAMPLEXY function. It runs much faster than SAMPLEXY, since it does no interpolation. It returns the function value at the grid point closest to each point in XPTS, YPTS. It is less accurate than SAMPLEXY, but may give adequate results in a much shorter time for large samples.
Example: compare with SAMPLEXY output
yes? USE levitus_climatology
yes? LET xlon = 234.5 + I[I=1:20]
yes? LET dely = 24./19
yes? LET ylat = 24.5 - dely*i[i=1:20] + dely
yes? LET a = samplexy(salt[X=200:300,Y=0:30,K=1], xlon, ylat)
yes? LET b = samplexy_closest(salt[X=200:300,Y=0:30,K=1], xlon, ylat)
yes? LIST a, b
DATA SET: /home/porter/tmap/ferret/linux/fer_dsets/data/levitus_climatology.cdf
X: 0.5 to 20.5
DEPTH (m): 0
Column 1: A is SAMPLEXY(SALT[X=200:300,Y=0:30,K=1], XLON, YLAT)
Column 2: B is SAMPLEXY_CLOSEST(SALT[X=200:300,Y=0:30,K=1], XLON, YLAT)
A B
1 / 1: 34.22 34.22
2 / 2: 34.28 34.26
3 / 3: 34.35 34.39
4 / 4: 34.41 34.43
5 / 5: 34.44 34.44
6 / 6: 34.38 34.40
7 / 7: 34.26 34.22
8 / 8: 34.09 34.07
9 / 9: 33.90 33.92
10 / 10: 33.74 33.78
11 / 11: 33.64 33.62
12 / 12: 33.63 33.62
13 / 13: 33.69 33.67
14 / 14: 33.81 33.75
15 / 15: 33.95 34.00
16 / 16: 34.11 34.11
17 / 17: 34.25 34.22
18 / 18: 34.39 34.33
19 / 19: 34.53 34.56
20 / 20: 34.65 34.65
SAMPLEXY_CURV Returns data which is on a curvilinear grid, sampled at a set of (X,Y) points, using interpolation.
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample |
|
DAT_LON |
Longitude coordinates of the curvilinear grid |
|
|
DAT_LAT |
Latitude coordinates of the curvilinear grid |
|
|
XPTS |
X values of sample points |
|
|
YPTS |
Y values of sample points |
|
|
Result Axes: |
X |
ABSTRACT; length same as XPTS and YPTS |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
Note: SAMPLEXY_CURV is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the first argument rather than a SET REGION command. See the discussion of grid-changing functions.
Example 1:
yes? USE curvi_data.nc
yes? SHADE u, geolon, geolat
! Define a set of locations. Note that the X values
! must be in the range of x coordinate values from the
! variable geolon. The function does not wrap values
! around to other modulo longitude values.
yes? LET xpts = {-111, -110, -6, 0, 43, 51}
yes? LET ypts = { -9, -8, -6,-2, -3, -4}
! check how the points overlay on the original grid
yes? PLOT/VS/OVER xpts, ypts
! this will list the U values at the (xpts,ypts) locations
yes? LIST SAMPLEXY_CURV(u, geolon, geolat, xpts, ypts)
Example 2:
! This method can be used to sample data on a grid of values ! Note it can be slow if you choose to sample at a lot of points. ! The CURV_TO_RECT functions may be a better choice in that case. yes? DEFINE AXIS/X=-200:-100:5 newx yes? DEFINE AXIS/Y=-20:20:1 newy ! Define variables containing all the x points at each y level, ! and likewise for y at each x yes? LET xpts = x[gx=newx] + 0*y[gy=newy] yes? LET ypts = 0*x[gx=newx] + y[gy=newy] ! The last 2 arguments to SAMPLEXY_CURV are 1D lists yes? LET xsample = xsequence(xpts) yes? LET ysample = xsequence(ypts) ! Check how the points overlay on the curvilienar data yes? PLOT/VS/OVER xsample, ysample ! upts is a list of values at the (xsample,ysample) locations yes? LET upts = SAMPLEXY_CURV(u, geolon, geolat, xsample, ysample) ! Put this onto the 2D grid defined by the new axes. yes? LET/TITLE="U sampled to new grid"/UNITS="`u,return=units`" \ u_on_newgrid = RESHAPE(upts, xpts) yes? SET WIN/NEW yes? SHADE u_on_newgrid
Ferret includes a number of SCAT2GRID functions which take a set of scattered locations in 2 dimensions, a grid definition, and interpolate data at the scattered locations to a grid. See below for the rest of the SCAT2GRIDGAUSS functions, followed by the SCAT2GRIDLAPLACE functions. Also see Appendix A for functions that use binning to put data onto a grid: SCAT2GRID_BIN_XY, and the count of scattered data used in a gridding operation: SCAT2GRID_NBIN_XY and SCAT2GRID_NOBS_XY. These binning functions also have XYT versions.
Discrete Sampling Geometries (DSG) data:
Observational data from DSG datasets contain collections of data which while not truly scattered, has lists of coordinate information that can feed into these functions for gridding into a multi-dimensional grid. However, with the exception of trajectory data the coordinates do not all have the same dimensionality. Timeseries data for instance has a station location for each station, and multiple observations in time. Profile data has station location and time, and multiple heights/depths in each profile. For the SCAT2GRID functions we need all of the first arguments, the "scattered" locations and observation, to be of the same size. We need to expand the station data to repeat the station location for each time in that station's time series.
The FAQ, Calling SCAT2GRID functions for DSG data explains how to work with these datasets.
SCAT2GRIDGAUSS_XY(XPTS, YPTS, F, XCOORD, YCOORD, XSCALE, YSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to an XY grid
|
Arguments: |
XPTS |
x-locations of scattered input triples, organized as a 1D list on any axis. |
|
YPTS |
y-locations of scattered input triples, organized as a 1D list on any axis. |
|
|
F |
F-data: 3rd component of scattered input triples. This is the variable we are putting onto the grid. It must have the scattered-data direction along an X or Y axis. May be fcn of Z, time, E, or F. |
|
|
XAXPTS |
coordinates of X-axis of output grid. Must be regularly spaced. |
|
|
YAXPTS |
coordinates of Y-axis of output grid. Must be regularly spaced. |
|
|
XSCALE |
Mapping scale for Gaussian weights in X direction, in data units (e.g. lon or m). See the discussion below. |
|
|
YSCALE |
Mapping scale for Gaussian weights in Y direction, in data units (e.g. lat or m) |
|
|
CUTOFF |
Cutoff for weight function. Only scattered points within CUTOFF*XSCALE and CUTOFF*YSCALE of the grid box center are included in the sum for the grid box. |
|
|
0 |
An unused argument: previously there had been a second "cutoff" argument but it was redundant. There is only one cutoff in the algorithm once the XSCALE and YSCALE mapping is applied. In future versions of Ferret this argument will be removed. |
|
|
Result Axes: |
X |
Inherited from XAXPTS |
|
Y |
Inherited from YAXPTS |
|
|
Z |
Inherited from F |
|
|
T |
Inherited from F |
Note:
The SCAT2GRIDGAUSS functions are "grid-changing" functions; the output grid is different from the input arguments. Therefore it is best to use explicit limits on any of the arguments rather than a SET REGION command. See the discussion of grid-changing functions.
Quick example:
yes? DEFINE AXIS/X=180:221:1 xax yes? DEFINE AXIS/Y=-30:10:1 yax yes? ! read some data yes? SET DATA/EZ/VARIABLES="times,lats,lons,var" myfile.dat yes? LET my_out = SCAT2GRIDGAUSS_XY(lons, lats, var, x[gx=xax], y[gy=yax], 2, 2, 2, 0)
If the output X axis is a modulo longitude axis, then the scattered X values should lie within the range of the actual coordinates of the axis. That is, if the scattered X values are xpts={355, 358, 2, 1, 352, 12} and the coordinates of the X axis you wish to grid to are longitudes of x=20,23,25,...,379 then you should apply a shift to your scattered points:
yes? USE levitus_climatology ! output will be on the grid of SALT yes? LET xx = x[gx=salt] yes? LET x1 = if lons lt `xx[x=@min]` then lons+360 yes? LET xnew = if x1 gt `xx[x=@max] then x1-360 else x1 yes? LET my_out = SCAT2GRIDGAUSS_XY(xnew, ypts, var, x[gx=xax], y[gy=yax], 2, 2, 2, 0)
The SCAT2GRIDGAUSS* functions use 1a Gaussian interpolation method to map irregular locations (xn, yn) to a regular grid (x0, y0). The output grid must have equally-spaced gridpoints in both the x and y directions. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
In addition, see the FAQ, Calling SCAT2GRID functions for DSG data explains how to work with these datasets.
Parameters for a square grid and a fairly dense distribution of scattered points relative to the grid might be XSCALE=YSCALE = 0.5, and CUTOFF = 2. To get better coverage, use a coarser grid or increase XSCALE, YSCALE and/or CUTOFF.
The value of the gridded function F at each grid point (x0, y0) is computed by:
F(x0,y0) = S(n=1 to Np)F(xn,yn)W(xn,yn) / S(n=1 to Np)W(xn,yn)
Where Np is the total number of irregular points within the "influence region" of a particular grid point, (determined by the CUTOFF parameter, defined below). The Gaussian weight fucntion Wn is given by
Wn(xn,yn) = exp{-[(xn-x0)2/(X)2 + (yn-y0)2/(Y)2]}
X and Y in the denominators on the right hand side are the mapping scales, arguments XSCALE and YSCALE.
The weight function has a nonzero value everywhere, so all of the scattered points in theory could be part of the sum for each grid point. To cut computation, the parameter CUTOFF is employed. If a cutoff of 2 is used (e.g. CUTOFF* XSCALE=2), then the weight function is set to zerowhen Wn< e-4. This occurs where distances from the grid point are less than 2 times the mapping scales X or Y.
(Reference for this method: Kessler and McCreary, 1993: The Annual Wind-driven Rossby Wave in the Subthermocline Equatorial Pacific, Journal of Physical Oceanography 23, 1192 -1207)
SCAT2GRIDGAUSS_XZ(XPTS, ZPTS, F, XAXPTS, ZAXPTS, XSCALE, ZSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to an XZ grid
See the description under SCAT2GRIDGAUSS_XY. Note that the output grid must have equally-spaced gridpoints in both the x and z directions.
SCAT2GRIDGAUSS_XT(XPTS, TPTS, F, XAXPTS, TAXPTS, XSCALE, TSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to an XT grid
See the description under SCAT2GRIDGAUSS_XY. Note that the output grid must have equally-spaced gridpoints in both the x and z directions.
SCAT2GRIDGAUSS_YZ(YPTS, ZPTS, F, YAXPTS, ZAXPTS, YSCALE, ZSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to a YZ grid
See the description under SCAT2GRIDGAUSS_XY. Note that the output grid must have equally-spaced gridpoints in both the y and z directions.
SCAT2GRIDGAUSS_YT(YPTS, TPTS, F, YAXPTS, TAXPTS, YSCALE, TSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to a YT grid
See the description under SCAT2GRIDGAUSS_XY. Note that the output grid must have equally-spaced gridpoints in both the y and z directions.
SCAT2GRIDGAUSS_ZT(ZPTS, TPTS, F, ZAXPTS, TAXPTS, ZSCALE, TSCALE, CUTOFF, 0) Use Gaussian weighting to grid scattered data to a ZT grid
See the description under SCAT2GRIDGAUSS_XY. Note that the output grid must have equally-spaced gridpoints in both the y and z directions.
Ch3 Sec2.3. SCAT2GRIDLAPLACE_XY
SCAT2GRIDLAPLACE_XY(XPTS, YPTS, F, XAXPTS, YAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an XY grid.
|
Arguments: |
XPTS |
x--locations of scattered input triples, organized as a 1D list on any axis. |
|
YPTS |
y-locations of scattered input triples, organized as a 1D list on any axis. |
|
|
F |
F-data: 3rd component of scattered input triples. This is the variable we are putting onto the grid. It must have the scattered-data direction along an X or Y axis. May be fcn of Z, time, E, or F. |
|
|
XAXPTS |
coordinates of X-axis of output grid. Must be regularly spaced. |
|
|
YAXPTS |
coordinates of Y-axis of output grid. Must be regularly spaced. |
|
|
CAY |
Amount of spline equation (between 0 and inf.) vs Laplace interpolation |
|
|
NRNG |
Grid points more than NRNG grid spaces from the nearest data point are set to undefined. |
|
|
Result Axes: |
X |
Inherited from XAXPTS |
|
Y |
Inherited from YAXPTS |
|
|
Z |
Inherited from F |
|
|
T |
Inherited from F |
Note:
The SCAT2GRIDLAPLACE functions are "grid-changing" functions; the output grid is different from the input arguments. Therefore it is best to use explicit limits on any of the arguments rather than a SET REGION command. See the discussion of grid-changing functions.
Quick example:
yes? DEFINE AXIS/X=180:221:1 xax yes? DEFINE AXIS/Y=-30:10:1 yax yes? ! read some data yes? SET DATA/EZ/VARIABLES="times,lats,lons,var" myfile.dat yes? LET my_out = SCAT2GRIDLAPLACE_XY(lons, lats, var, x[gx=xax], y[gy=yax], 2., 5) yes? SHADE my_out
If the output X axis is a modulo longitude axis, then the scattered X values should lie within the range of the actual coordinates of the axis. That is, if the scattered X values are xpts={355, 358, 2, 1, 352, 12} and the coordinates of the X axis you wish to grid to are longitudes of x=20,23,25,...,379 then you should apply a shift to your scattered points:
yes? USE levitus_climatology ! output will be on the grid of SALT yes? LET xx = x[gx=salt] yes? LET x1 = if lons lt `xx[x=@min]` then lons+360 yes? LET xnew = if x1 gt `xx[x=@max] then x1-360 else x1 yes? LET my_out = SCAT2GRIDLAPLACE_XY(xnew, lats, var, x[gx=xax], y[gy=yax], 2., 5)
For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
In addition, see the FAQ, Calling SCAT2GRID functions for DSG data explains how to work with these datasets.
The SCAT2GRIDLAPLACE* functions employ the same interpolation method as is used by PPLUS, and appears elsewhere in Ferret, e.g. in contouring. The parameters are used as follows (quoted from the PPLUS Users Guide. A reference for this is "Plot Plus, a Scientific Graphics System", written by Donald W. Denbo, April 8, 1987.):
CAY
If CAY=0.0, Laplacian interpolation is used. The resulting surface tends to have rather sharp peaks and dips at the data points (like a tent with poles pushed up into it). There is no chance of spurious peaks appearing. As CAY is increased, Spline interpolation predominates over the Laplacian, and the surface passes through the data points more smoothly. The possibility of spurious peaks increases with CAY. CAY= infinity is pure Spline interpolation. An over relaxation process in used to perform the interpolation. A value of CAY=5 often gives a good surface.
NRNG
Any grid points farther than NRNG away from the nearest data point will be set to "undefined" The default used by PPLUS is NRNG = 5
Ch3 Sec2.3. SCAT2GRIDLAPLACE_XZ
SCAT2GRIDLAPLACE_XZ(XPTS, ZPTS, F, XAXPTS, ZAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an XZ grid.
The gridding algorithm is discussed under SCAT2GRIDLAPLACE_XY. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
Ch3 Sec2.3 SCAT2GRIDLAPLACE_XT
SCAT2GRIDLAPLACE_XT(XPTS, TPTS, F, XAXPTS, TAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an XT grid.
The gridding algorithm is discussed under SCAT2GRIDLAPLACE_XY. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
Ch3 Sec2.3 SCAT2GRIDLAPLACE_YT
SCAT2GRIDLAPLACE_YT(YPTS, TPTS, F, YAXPTS, TAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to a YT grid.
The gridding algorithm is discussed under SCAT2GRIDLAPLACE_XY. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
Ch3 Sec2.3 SCAT2GRIDLAPLACE_YZ
SCAT2GRIDLAPLACE_YZ(YPTS, ZPTS, F, YAXPTS, ZAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an YZ grid.
The gridding algorithm is discussed under SCAT2GRIDLAPLACE_XY. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
How to use Ferret External Functions for gridding scattered data points
Ch3 Sec2.3 SCAT2GRIDLAPLACE_ZT
SCAT2GRIDLAPLACE_ZT(ZPTS, TPTS, F, ZAXPTS, TAXPTS, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to a ZT grid.
The gridding algorithm is discussed under SCAT2GRIDLAPLACE_XY. For examples of the gridding functions, run the script objective_analysis_demo, or see the on-line demonstration
Note:
Discrete Sampling Geometries (DSG) data:
Observational data from DSG datasets contain collections of data which while not truly scattered, has lists of coordinate information that can feed into these functions for gridding into a multi-dimensional grid. However, with the exception of trajectory data the coordinates do not all have the same dimensionality. Timeseries data for instance has a station location for each station, and multiple observations in time. Profile data has station location and time, and multiple heights/depths in each profile. For the SCAT2GRID functions we need all of the first arguments, the "scattered" locations and observation, to be of the same size. We need to expand the station data to repeat the station location for each time in that station's time series.
The FAQ, Calling SCAT2GRID functions for DSG data explains how to work with these datasets.
How to use Ferret External Functions for gridding scattered data points
SORTI(DAT): Returns indices of data, sorted on the I axis in increasing order
SORTI_STR(DAT): returns indices of data, sorted on the I axis in increasing order. If SORTI is called with a string variable as the argument. SORTI_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
ABSTRACT, same length as DAT x-axis |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
SORTI, SORTJ, SORTK, SORTL, SORTM, and SORTN return the indices of the data after it has been sorted. These functions are used in conjunction with functions such as the SAMPLE functions to do sorting and sampling. See the demonstration ef_sort_demo.jnl for common useage of these functions.
As with other functions which change axes, specify any region information for the variable DAT explicitly in the function call. See the discussion of grid-changing functions.
SORTJ(DAT) Returns indices of data, sorted on the I axis in increasing order
SORTJ_STR(DAT): returns indices of data, sorted on the J axis in increasing order. If SORTJ is called with a string variable as the argument, SORTJ_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
ABSTRACT, same length as DAT y-axisInherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
See the discussion under SORTI
SORTK(DAT) Returns indices of data, sorted on the I axis in increasing order
SORTK_STR(DAT): returns indices of data, sorted on the K axis in increasing order. If SORTK is called with a string variable as the argument, SORTK_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
ABSTRACT, same length as DAT z-axis |
|
|
T |
Inherited from DAT |
See the discussion under SORTI
SORTL(DAT) Returns indices of data, sorted on the L axis in increasing order
SORTL_STR(DAT): returns indices of data, sorted on the L axis in increasing order. If SORTL is called with a string variable as the argument, SORTL_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
ABSTRACT, same length as DAT t-axis |
See the discussion under SORTI
SORTM(DAT) Returns indices of data, sorted on the M axis in increasing order
SORTM_STR(DAT): returns indices of data, sorted on the M axis in increasing order. If SORTM is called with a string variable as the argument, SORTM_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
|
|
E |
ABSTRACT, same length as DAT e-axis |
|
|
F |
Inherited from DAT |
See the discussion under SORTI
SORTN(DAT) Returns indices of data, sorted on the N axis in increasing order
SORTN_STR(DAT): returns indices of data, sorted on the N axis in increasing order. If SORTN is called with a string variable as the argument, SORTN_STR is run by Ferret.
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
|
|
E |
Inherited from DAT |
|
|
F |
ABSTRACT, same length as DAT f-axis |
See the discussion under SORTI
TAUTO_COR(A): Compute autocorrelation function (ACF) of time series, lags of 0,...,N-1, where N is the length of the time axis.
|
Arguments: |
A |
A function of time, and perhaps x,y,z |
|
Result Axes: |
X |
Inherited from A |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
ABSTRACT, same length as A time axis (lags) |
Note:
TAUTO_COR is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the first argument rather than a SET REGION command. See the discussion of grid-changing functions.
XAUTO_COR(A): Compute autocorrelation function (ACF) of a series in X, lags of 0,...,N-1, where N is the length of the x axis.
|
Arguments: |
A |
A function of x, and perhaps y,z,t |
|
Result Axes: |
X |
ABSTRACT, same length as X axis of A (lags) |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
Inherited from A |
Note:
XAUTO_COR is a "grid-changing" function; its output grid is different from the input arguments. Therefore it is best to use explicit limits on the first argument rather than a SET REGION command. See the discussion of grid-changing functions.
TAX_DAY(A, B): Returns days of month of time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE: The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See the examples in the discussion of the TAX_DATESTRING function
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example:
yes? use "http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/reynolds_sst_wk.nc"
yes? list/t=1-feb-1982:15-mar-1982 tax_day(t[gt=wsst], wsst[i=1,j=1])
VARIABLE : TAX_DAY (T[GT=WSST], WSST[I=1,J=1])
DATA SET : Reynolds Optimum Interpolation Weekly SST Analysis
FILENAME : reynolds_sst_wk.nc
FILEPATH : http://ferret.pmel.noaa.gov/thredds/dodsC/data/PMEL/
SUBSET : 7 points (TIME)
02-FEB-1982 00 / 5: 2.00
09-FEB-1982 00 / 6: 9.00
16-FEB-1982 00 / 7: 16.00
23-FEB-1982 00 / 8: 23.00
02-MAR-1982 00 / 9: 2.00
09-MAR-1982 00 / 10: 9.00
16-MAR-1982 00 / 11: 16.00
TAX_DAYFRAC(A, B): Returns fraction of day from time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE: The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See the examples in the discussion of the TAX_DATESTRING function.
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example: Show both the TAX_DATESTRING and TAX_DAYFRAC output. Because this is a climatological axis, there are no years in the dates.
yes? use coads_climatology
yes? let tt = t[gt=sst, L=1:5]
yes? let tvar = sst[x=180,y=0]
yes? list tax_datestring(tt, tvar, "hour"), tax_dayfrac(tt,tvar)
DATA SET: /home/users/tmap/ferret/linux/fer_dsets/data/coads_climatology.cdf
TIME: 01-JAN 00:45 to 01-JUN 05:10
Column 1: EX#1 is TAX_DATESTRING(TT, TVAR, "hour")
Column 2: EX#2 is TAX_DAYFRAC(TT,TVAR)
EX#1 EX#2
16-JAN / 1: "16-JAN 06" 0.2500
15-FEB / 2: "15-FEB 16" 0.6869
17-MAR / 3: "17-MAR 02" 0.1238
16-APR / 4: "16-APR 13" 0.5606
16-MAY / 5: "16-MAY 23" 0.9975
TAX_JDAY(A, B): Returns day of year from time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE 1:The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See also the examples in the discussion of the TAX_DATESTRING function.
NOTE 2: This function currently returns the date relative to a Standard (Gregorian) calendar. If the time axis is on a different calendar this is NOT taken into account. This will be fixed in a future Ferret release.
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example:
yes? use coads_climatology
yes? list tax_jday(t[gt=sst], sst[i=1,j=1])
VARIABLE : TAX_JDAY(T[GT=SST], SST[I=1,J=1])
FILENAME : coads_climatology.cdf
FILEPATH : /home/porter/tmap/ferret/linux/fer_dsets/data/
SUBSET : 12 points (TIME)
16-JAN / 1: 16.0
15-FEB / 2: 46.0
17-MAR / 3: 77.0
16-APR / 4: 107.0
16-MAY / 5: 137.0
16-JUN / 6: 168.0
16-JUL / 7: 198.0
16-AUG / 8: 229.0
15-SEP / 9: 259.0
16-OCT / 10: 290.0
15-NOV / 11: 320.0
16-DEC / 12: 351.0
TAX_MONTH(A, B): Returns months from time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE: The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See also the examples in the discussion of the TAX_DATESTRING function.
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example:
yes? use "http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/reynolds_sst_wk.nc"
yes? list/t=18-jan-1982:15-mar-1982 tax_month(t[gt=wsst], wsst[i=1,j=1])
VARIABLE : TAX_MONTH(T[GT=WSST], WSST[I=1,J=1])
DATA SET : Reynolds Optimum Interpolation Weekly SST Analysis
FILENAME : reynolds_sst_wk.nc
FILEPATH : http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/
SUBSET : 9 points (TIME)
19-JAN-1982 00 / 3: 1.000
26-JAN-1982 00 / 4: 1.000
02-FEB-1982 00 / 5: 2.000
09-FEB-1982 00 / 6: 2.000
16-FEB-1982 00 / 7: 2.000
23-FEB-1982 00 / 8: 2.000
02-MAR-1982 00 / 9: 3.000
09-MAR-1982 00 / 10: 3.000
16-MAR-1982 00 / 11: 3.000
TAX_UNITS(A): Returns units from time axis coordinate values, in seconds
|
Arguments: |
A |
variable with reference time axis |
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE: to get the time units as a string use the RETURN=tunits keyword (p. )
Example:
yes? use "http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/reynolds_sst_wk.nc"
yes? say `wsst,return=tunits`
!-> MESSAGE/CONTINUE DAYS
DAYS
yes? list tax_units(t[gt=wsst])
VARIABLE : TAX_UNITS(T[GT=WSST])
DATA SET : Reynolds Optimum Interpolation Weekly SST Analysis
FILENAME : reynolds_sst_wk.nc
FILEPATH : http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/
86400.
TAX_YEAR(A, B): Returns years of time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE :The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See also the examples in the discussion of the TAX_DATESTRING function.
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example:
yes? use "http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/COADS/coads_sst.cdf"
yes? list/L=1403:1408 tax_year(t[gt=sst], sst[i=1,j=1])
VARIABLE : TAX_YEAR(T[GT=SST], SST[K=1,J=1])
DATA SET : COADS Surface Marine Observations (1854-1993)
FILENAME : coads_sst.cdf
FILEPATH : http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/COADS/
SUBSET : 6 points (TIME)
15-NOV-1970 00 / 1403: 1970.
15-DEC-1970 00 / 1404: 1970.
15-JAN-1971 00 / 1405: 1971.
15-FEB-1971 00 / 1406: 1971.
15-MAR-1971 00 / 1407: 1971.
15-APR-1971 00 / 1408: 1971.
TAX_YEARFRAC(A, B): Returns fraction of year of time axis coordinate values
|
Arguments: |
A |
time steps to convert |
|
B |
variable with reference time axis; use region settings to restrict this to a small region (see below) |
|
|
Result Axes: |
X |
normal |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
Inherited from A |
NOTE: The variable given for argument 2 is loaded into memory by this function, so restrict its range in X, Y, and/or Z so that it is not too large. Or, if you are getting the time steps from the variable, specify the time steps for both arguments. See also the examples in the discussion of the TAX_DATESTRING function.
[Caution: Previous to Ferret v6.8 only: Although Ferret stores and computes with coordinate values in double-precision, argument 1 of this function is a single-precision variable. This function translates the values in argument 1 to the nearest double-precision coordinate value of the time axis of argument 2 when possible. If the truncation to single precision in an expression t[gt=var] has resulted in duplicate single-precision values the function will return an error message. See the discussion under TAX_DATESTRING.] With Ferret v6.8 and after, all calculations are done in double precision and this is not a problem.
Example:
yes? use "http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/COADS/coads_sst.cdf"
yes? list/L=1403:1408 tax_yearfrac(t[gt=sst], sst[i=1,j=1])
VARIABLE : TAX_YEARFRAC(T[GT=SST], SST[K=1,J=1])
DATA SET : COADS Surface Marine Observations (1854-1993)
FILENAME : coads_sst.cdf
FILEPATH : http://ferret.pmel.noaa.gov/pmel/thredds/dodsC/data/PMEL/PMEL/COADS/
SUBSET : 6 points (TIME)
15-NOV-1970 00 / 1403: 0.8743
15-DEC-1970 00 / 1404: 0.9563
15-JAN-1971 00 / 1405: 0.0410
15-FEB-1971 00 / 1406: 0.1257
15-MAR-1971 00 / 1407: 0.2049
15-APR-1971 00 / 1408: 0.2896
Chapter 3, Section 2.3 MINMAX
MINMAX(A): Returns the minimum and maximum of the argument
|
Arguments: |
A |
variable to find the extrema |
|
Result Axes: |
X |
abstract: length 2 |
|
Y |
normal |
|
|
Z |
normal |
|
|
T |
normal |
The result is returned on a 2-point abstract axis, with result[i=1]=min, result[i=1]=max
Example:
yes? let v = {1,4,56,8,12,14,,-0.5}
yes? list MINMAX(v)
VARIABLE : MINMAX(V)
SUBSET : 2 points (X)
1 / 1: -0.50
2 / 2: 56.00
Chapter 3, Section 2.4 TRANSFORMATIONS
Transformations (e.g., averaging, integrating, etc.) may be specified along the axes of a variable. Some transformations (e.g., averaging, minimum, maximum) reduce a range of data to a point; others (e.g., differentiating or smoothers) retain the range.
When transformations are specified along more than one axis of a single variable the order of execution is X axis first, then Y, Z, T, E, and F.
The regridding transformations are described in the chapter "Grids and Regions" ).
Example syntax: TEMP[Z=0:100@LOC:20] (depth at which temp has value 20)
Valid transformations are
|
Transform |
Default |
Description |
|
@DIN |
definite integral (weighted sum) |
|
|
@IIN |
indefinite integral (weighted running sum) |
|
|
@ITP |
linear interpolation |
|
|
@AVE |
average |
|
|
@VAR |
unweighted variance |
|
|
@STD |
standard deviation |
|
|
@MIN |
minimum |
|
|
@MAX |
maximum |
|
| @MED | 3 pt | median smoothed |
| @SMN | 3 pt | minimum smoothed, using min |
| @SMX | 3 pt | maximum smoothed, using max |
|
@SHF |
1 pt |
shift |
|
@SBX |
3 pt |
boxcar smoothed |
|
@SBN |
3 pt |
binomial smoothed |
|
@SHN |
3 pt |
Hanning smoothed |
|
@SPZ |
3 pt |
Parzen smoothed |
|
@SWL |
3 pt |
Welch smoothed |
|
@DDC |
centered derivative |
|
|
@DDF |
forward derivative |
|
|
@DDB |
backward derivative |
|
|
@NGD |
number of valid points |
|
|
@NBD |
number of bad (invalid) points flagged |
|
|
@SUM |
unweighted sum |
|
|
@RSUM |
running unweighted sum |
|
|
@FAV |
3 pt |
fill missing values with average |
|
@FLN |
1 pt |
fill missing values by linear interpolation |
|
@FNR |
1 pt |
fill missing values with nearest point |
|
@LOC |
0 |
coordinate of ... (e.g., depth of 20 degrees) |
|
@WEQ |
"weighted equal" (integrating kernel) |
|
|
@CDA |
closest distance above |
|
|
@CDB |
closest distance below |
|
|
@CIA |
closest index above |
|
|
@CIB |
closest index below |
The command SHOW TRANSFORM will produce a list of currently available transformations.
|
U[Z=0:100@AVE] |
– average of u between 0 and 100 in Z |
|
sst[T=@SBX:10] |
– box-car smooths sst with a 10 time point filter |
|
tau[L=1:25@DDC] |
– centered time derivative of tau |
|
v[L=@IIN] |
– indefinite (accumulated) integral of v |
|
qflux[X=@AVE,Y=@AVE] |
– XY area-averaged qflux |
General information about transformations
Transformations are normally computed axis by axis; if multiple axes have transformations specified simultaneously (e.g., U[Z=@AVE,L=@SBX:10]) the transformations will be applied sequentially in the order X then Y then Z then T, E, and F. There are a few exceptions to this: if @DIN is applied simultaneously to both the X and Y axes (in units of degrees of longitude and latitude, respectively) the calculation will be carried out on a per-unit-area basis (as a true double integral) instead of a per-unit-length basis, sequentially. This ensures that the COSINE(latitude) factors will be applied correctly. The same applies to @AVE, @VAR, and @STD simultaneously on X and Y as well as @NGD and @NBD for any combination of directions on the variable's grid.
If one of the multiple-direction transformations (AVE, DIN, VAR, STD, NGD, NBD) is specified, but the grid contains only one of those directions, the 1-dimensional transformation is computed instead. (Prior to Ferret v7.41, when one of the multi-direction transformations was requested, say an XY average, Ferret required that the grid has an x and a y axis.) For all transformations that operate axis by axis, a transformation specified for any axis not on the grid is ignored.
Data that are flagged as invalid are excluded from calculations.
All integrations and averaging are accomplished by multiplying the width of each grid box or portion of the box by the value of the variable in that grid box—then summing and dividing as appropriate for the particular transformation.
If integration or averaging limits are given as world coordinates, the grid boxes at the edges of the region specified are weighted according to the fraction of grid box that actually lies within the specified region. If the transformation limits are given as subscripts, the full box size of each grid point along the axis is used—including the first and last subscript given. The region information that is listed with the output reflects this.
Some transformations (derivatives, shifts, smoothers) require data points from beyond the edges of the indicated region in order to perform the calculation. Ferret automatically accesses this data as needed. It flags edge points as missing values if the required beyond-edge points are unavailable (e.g., @DDC applied on the X axis at I=1).
When calculating integrals and derivatives (@IIN, @DIN, @DDC, @DDF, and @DDB) Ferret attempts to use standardized units for the grid coordinates. If the underlying axis is in a known unit of length Ferret converts grid box lengths to meters. If the underlying axis is in a known unit of time Ferret converts grid box lengths to seconds, using the definition for the calendar of that axis. If the underlying axis is degrees of longitude a factor of COSINE (latitude) is applied to the grid box lengths in meters.
If the underlying axis units are unknown Ferret uses those unknown units for the grid box lengths. (If Ferret does not recognize the units of an axis it displays a message to that effect when the DEFINE AXIS or SET DATA command defines the axis.) See command DEFINE AXIS/UNITS in the Commands Reference in this manual for a list of recognized units.
Version 7.6 includes support for Discrete Sampling Geometries (DSG) datasets, containing collections of Timeseries, Profiles, Trajectories, and Points. When transformations are applied to data from a DSG file the transformation applies only within each feature. That is, for a collection of profiles the Maximum value or Indefinite Integral or Smoothing operation or Number of valid points is computed for one profile at a time with the calculation restarting on the next feature.
Chapter 3, Section 2.4.2
Transformations applied to irregular regions
Since transformations are applied along the orthogonal axes of a grid they lend themselves naturally to application over "rectangular" regions (possibly in 3 or 4 dimensions). Ferret has sufficient flexibility, however, to perform transformations over irregular regions.
Suppose, for example, that we wish to determine the average wind speed within an irregularly shaped region of the globe defined by a threshold sea surface temperature value. We can do this through the creation of a mask, as in this example:
yes? SET DATA coads_climatology yes? SET REGION/l=1/@t ! January in the Tropical Pacific yes? LET sst28_mask = IF sst GT 28 THEN 1 yes? LET masked_wind_speed = wspd * sst28_mask yes? LIST masked_wind_speed[X=@AVE,Y=@AVE]
The variable sst28_mask is a collection of 1's and missing values. Using it as a multiplier on the wind speed field produces a new result that is undefined except in the domain of interest.
When using masking be aware of these considerations:
- Use undefined values rather than zeros to avoid contaminating the calculation with zero values. The above commands where sst_mask_28 is defined with no ELSE statement, automatically implies "ELSE bad".
- If the data contains values that are exactly Zero, then "IF var" (comparison to the missing-flag for the variable) will be false when the data is missing and ALSO when its value is zero. This is because Ferret does not have a logical data type, and so zero is equivalent to FALSE. See the documentation on the IF syntax. To handle this case, you can get the missing-value for the variable and use it to define the expression.
yes? LET mask = IF var NE `var,RETURN=bad` THEN 1
- The masked region is composed of rectangles at the level of resolution of the gridded variables; the mask does NOT follow smooth contour lines. To obtain a smoother mask it may be desirable to regrid the calculation to a finer grid.
- Variables from different data sets can be used to mask one another. For example, the ETOPO60 bathymetry data set can be used to mask regions of land and sea.
General information about smoothing transformations
Ferret provides several transformations for smoothing variables (removing high frequency variability). These transformations replace each value on the grid to which they are applied with a weighted average of the surrounding data values along the axis specified. For example, the expression u[T=@SPZ:3] replaces the value at each (I,J,K,L) grid point of the variable "u" with the weighted average
u at t = 0.25*(u at t-1) + 0.5*(u at t) + 0.25*(u at t+1)
The various choices of smoothing transformations (@SBX, @SBN, @SPZ, @SHN, @SWL) represent different shapes of weighting functions or "windows" with which the original variable is convolved. New window functions can be obtained by nesting the simple ones provided. For example, using the definitions
yes? LET ubox = u[L=@SBX:15] yes? LET utaper = ubox[L=@SHN:7]
produces a 21-point window whose shape is a boxcar (constant weight) with COSINE (Hanning) tapers at each end.
Ferret may be used to directly examine the shape of any smoothing window: Mathematically, the shape of the smoothing window can be recovered as a variable by convolving it with a delta function. In the example below we examine (PLOT) the shape of a 15-point Welch window (Figure 3_4).
! define X axis as [-1,1] by 0.2 yes? GO unit_square yes? SET REGION/X=-1:1 yes? LET delta = IF X EQ 0 THEN 1 ELSE 0 ! convolve delta with Welch window yes? PLOT delta[I=@SWL:15]
Chapter 3, Section 2.4.4
@DIN—definite integral
The transformation @DIN computes the definite integral—a single value that is the integral between two points along an axis (compare with @IIN). It is obtained as the sum of the grid_box*variable product at each grid point. Grid points at the ends of the indicated range are weighted by the fraction of the grid box that falls within the integration interval.
If @DIN is specified simultaneously on multiple axes the calculation will be performed as a multiple integration rather than as sequential single integrations. The output will document this fact by indicating a transformation of "@IN4" or "XY integ." See the General Information on transformations for important details about this transformation. (In particular note that when the limits are given in index values, the transformation includes the entire interval of both endpoints; if it is given in world coordinates, it uses partial grid cells out to those world limits.)
Example:
yes? CONTOUR/X=160E:160W/Y=5S:5N u[Z=0:50@DIN]
In a latitude/longitude coordinate system X=@DIN is sensitive to the COS(latitude) correction.
Integration over complex regions in space may be achieved by masking the multi-dimensional variable in question and using the multi-dimensional form of @DIN. For example
yes? LET salinity_where_temp_gt_15 = IF temp GT 15 THEN salt
yes? LIST salinity_where_temp_gt_15[X=@DIN,Y=@DIN,Z=@DIN]
Chapter 3, Section 2.4.5
The transformation @IIN computes the indefinite integral—at each subscript of the result it is the value of the integral from the start value to the upper edge of that grid box. It is obtained as a running sum of the grid_box*variable product at each grid point. Grid points at the ends of the indicated range are weighted by the fraction of the grid box that falls within the integration interval. See the General Information on transformations for important details about this transformation.
In particular, it's important to pay attention to how the limits are specified. If the limits of integration are given as world coordinates (var[X=10:22@IIN]), the grid boxes at the edges of the region specified are weighted according to the fraction of grid box that actually lies within the specified region. If the transformation limits are given as subscripts (var[I=1:13@IIN]), then the full box size of each grid point along the axis is used—including the first and last subscript given.
Example:
yes? CONTOUR/X=160E:160W/Z=0 u[Y=5S:5N@IIN]
Note 1: The indefinite integral is always computed in the increasing coordinate direction. To compute the indefinite integral in the reverse direction use
LET reverse_integral = my_var[X=lo:hi@DIN] - my_var[X=lo:hi@IIN]
Note 2: In a latitude/longitude coordinate system X=@IIN is sensitive to the COS(latitude) correction.
Note 3: The result of the indefinite integral is shifted by 1/2 of a grid cell from its "proper" location. This is because the result at each grid cell includes the integral computed to the upper end of that cell. (This was necessary in order that var[I=lo:hi@DIN] and var[I=lo:hi@IIN] produce consistent results.)
To illustrate, consider these commands
yes? LET one = x-x+1 yes? LIST/I=1:3 one[I=@din] X-X+1 X: 0.5 to 3.5 (integrated) 3.000 yes? LIST/I=1:3 one[I=@iin] X-X+1 indef. integ. on X 1 / 1: 1.000 2 / 2: 2.000 3 / 3: 3.000
The grid cell at I=1 extends from 0.5 to 1.5. The value of the integral at 1.5 is 1.000 as reported but the coordinate listed for this value is 1 rather than 1.5. Two methods are available to correct for this 1/2 grid cell shift.
Method 1: correct the result by subtracting the 1/2 grid cell error
yes? LIST/I=1:3 one[I=@iin] - one/2 ONE[I=@IIN] - ONE/2 1 / 1: 0.500 2 / 2: 1.500 3 / 3: 2.500
Method 2: correct the coordinates by shifting the axis 1/2 of a grid cell
yes? DEFINE AXIS/X=1.5:3.5:1 xshift yes? LET SHIFTED_INTEGRAL = one[I=@IIN] yes? LET corrected_integral = shifted_integral[GX=xshift@ASN] yes? LIST/I=1:3 corrected_integral SHIFTED_INTEGRAL[GX=XSHIFT@ASN] 1.5 / 1: 1.000 2.5 / 2: 2.000 3.5 / 3: 3.000
Method 3: Use the @IIN regridding transformation (new in Ferret v7.4.2). When the destination axis for the regridding is the same as the source axis, The result of that transformation is 0 at the bottom of the first grid cell, and is equal to the definite integral at the top of the uppermost grid cell.
yes? define axis/x=1:3:1 x3ax
yes? let ones = one[gx=x3ax@asn]
! the transformation@IIN
yes? LIST ones[I=@iin]
VARIABLE : ONE[GX=X3AX@ASN]
indef. integ. on X
SUBSET : 3 points (X)
1 / 1: 1.000
2 / 2: 2.000
3 / 3: 3.000
! The regridding transformation, regrid to the source axis.
yes? LIST ones[gx=x3ax@iin]
VARIABLE : ONE[GX=X3AX@ASN]
regrid: 1 delta on X@IIN
SUBSET : 3 points (X)
1 / 1: 0.500
2 / 2: 1.500
3 / 3: 2.500
Chapter 3, Section 2.4.6
The transformation @AVE computes the average weighted by grid box size—a single number representing the average of the variable between two endpoints.
If @AVE is specified simultaneously on multiple axes the calculation will be performed as a multiple integration rather than as sequential single integrations. The output will document this fact by showing @AV4 or "XY ave" as the transformation.
See the General Information on transformations for important details about this transformation. In particular, note the discussion about specifying the averaging interval in world coordinates, e.g. longitude, meters, time as in var[x=3.4:4.6@AVE] versus specifying the interval using indices, as in var[I=4:12@AVE]. When the interval is expressed in world coordinates, the weighting is done using partial grid boxes at the edges of the interval. If the interval is expressed using indices, the entire grid cells contribute to the weights.
The @WGT transformation returns the weights used by @AVE
Example:
yes? CONTOUR/X=160E:160W/Y=5S:5N u[Z=0:50@AVE]
Note that the unweighted mean can be calculated using the @SUM and @NGD transformations.
Averaging over complex regions in space may be achieved by masking the multi-dimensional variable in question and using the multi-dimensional form of @AVE. For example
yes? LET salinity_where_temp_gt_15 = IF temp GT 15 THEN salt yes? LIST salinity_where_temp_gt_15[X=@AVE,Y=@AVE,Z=@AVE]
When we use var[x=@AVE] Ferret averages over the grid points of the variable along the X axis, using any region in X that is in place. IF a specified range is given X=x1:x2@ave, then Ferret uses portions of grid cells to average over that exact region.
yes? USE coads_climatology yes? LIST/L=1/Y=45 sst[x=301:305@AVE] VARIABLE : SEA SURFACE TEMPERATURE (Deg C) LONGITUDE: 59W to 55W (averaged) LATITUDE : 45N TIME : 16-JAN 06:00 2.6557 yes? LET var = sst[x=301:305] yes? LIST/L=1/Y=45 var VARIABLE : SST[X=301:305] SUBSET : 3 points (LONGITUDE) LATITUDE : 45N TIME : 16-JAN 06:00 45N 59W / 141: 2.231 57W / 142: 2.604 55W / 143: 3.183 yes? LIST/L=1/Y=45 var[x=@AVE] VARIABLE : SST[X=301:305] LONGITUDE: 60W to 54W (averaged) LATITUDE : 45N TIME : 16-JAN 06:00 2.6730
The last average is taken not from a specific X to another specific X, but over all grid cells in the range where the variable var is defined. Note in each listing the LONGITUDE range of the average.
Chapter 3, Section 2.4.7
@VAR—weighted variance
The transformation @VAR computes the weighted variance of the variable with respect to the indicated region (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986).
As with @AVE, if @VAR is applied simultaneously to multiple axes the calculation is performed as the variance of a block of data rather than as nested 1-dimensional variances. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.7A
STD—weighted standard deviation
The transformation @STD computes the weighted standard deviation of the variable with respect to the indicated region (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986).
As with @AVE, if @STD is applied simultaneously to multiple axes the calculation is performed as the standard deviation of a block of data rather than as nested 1-dimensional standard deviation computations. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.8
@MIN—minimum
The transformation @MIN finds the minimum value of the variable within the specified axis range. See the General Information on transformations for important details about this transformation.
Example:
For fixed Z and Y
yes? PLOT/T="1-JAN-1982":"1-JAN-1983" temp[X=160E:160W@MIN]
plots a time series of the minimum temperature found between longitudes 160 east and 160 west.
Chapter 3, Section 2.4.9
@MAX—maximum
The transformation @MAX finds the maximum value of the variable within the specified axis range. See also @MIN. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.10
@SHF:n—shift
The transformation @SHF shifts the data up or down in subscript by the number of points given as the argument. The default is to shift by 1 point. See the General Information on transformations for important details about this transformation.
Examples:
U[L=@SHF:2]
associates the value of U[L=3] with the subscript L=1.
U[L=@SHF:1]-U
gives the forward difference of the variable U along the L axis.
Chapter 3, Section 2.4.11
@SBX:n—boxcar smoother
The transformation @SBX applies a boxcar window (running mean) to smooth the variable along the indicated axis. The width of the boxcar is the number of points given as an argument to the transformation. The default width is 3 points. All points are weighted equally, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If the number of points specified is even, however, @SBX weights the end points of the boxcar smoother as ½. See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0 u[L=1:120@SBX:5]
The transformation @SBX does not reduce the number of points along the axis; it replaces each of the original values with the average of its surrounding points. Regridding can be used to reduce the number of points.
Chapter 3, Section 2.4.12
@SBN:n—binomial smoother
The transformation @SBN applies a binomial window to smooth the variable along the indicated axis. The width of the smoother is the number of points given as an argument to the transformation. The default width is 3 points. The weights are applied without regard to the widths of the grid boxes, making this transformation best suited to axes with equally spaced points. See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@SBN:15]
The transformation @SBN does not reduce the number of points along the axis; it replaces each of the original values with a weighted sum of its surrounding points. Regridding can be used to reduce the number of points. The argument specified with @SBN, the number of points in the smoothing window, must be an odd value; an even value would result in an effective shift of the data along its axis.
Chapter 3, Section 2.4.13
@SHN:n—Hanning smoother
Transformation @SHN applies a Hanning window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. Note that the Hanning window used by Ferret contains only non-zero weight values with the window width.The default width is 3 points. Some interpretations of this window function include zero weights at the end points. Use an argument of N-2 to achieve this effect (e.g., @SBX:5 is equivalent to a 7-point Hanning window which has zeros as its first and last weights). See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.14
@SPZ:n—Parzen smoother
Transformation @SPZ applies a Parzen window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. The default window width is 3 points. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.15
@SWL:n—Welch smoother
Transformation @SWL applies a Welch window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. The default window width is 3 points. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.16
@DDC—centered derivative
The transformation @DDC computes the derivative with respect to the indicated axis using a centered differencing scheme. The units of the underlying axis are treated as they are with integrations. If the points of the axis are unequally spaced, note that the calculation used is still (Fi+1 – Fi–1) / (Xi+1 – Xi–1) . See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDC]
Chapter 3, Section 2.4.17
@DDF—forward derivative
The transformation @DDF computes the derivative with respect to the indicated axis. A forward differencing scheme is used. The units of the underlying axis are treated as they are with integrations. See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDF]
Chapter 3 Section 2.4.18
@DDB—backward derivative
The transformation @DDF computes the derivative with respect to the indicated axis. A backward differencing scheme is used. The units of the underlying axis are treated as they are with integrations. See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDB]
Chapter 3, Section 2.4.19
@NGD—number of good points
The transformation @NGD computes the number of good (valid) points of the variable with respect to the indicated axis. Use @NGD in combination with @SUM to determine the number of good points in a multi-dimensional region.
This transformation may be applied to string variables; if there are null strings in the variable those are treated as missing.
Note that, as with @AVE, when @NGD is applied simultaneously to multiple axes the calculation is applied to the entire block of values rather than to the individual axes. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.20
The transformation @NBD computes the number of bad (invalid) points of the variable with respect to the indicated axis. Use @NBD in combination with @SUM to determine the number of bad points in a multi-dimensional region.
This transformation may be applied to string variables; if there are null strings in the variable those are treated as missing.
Note that, as with @AVE, when @NBD is applied simultaneously to multiple axes the calculation is applied to the entire block of values rather than to the individual axes. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.21
@SUM—unweighted sum
The transformation @SUM computes the unweighted sum (arithmetic sum) of the variable with respect to the indicated axis. This transformation is most appropriate for regions specified by subscript. If the region is specified in world coordinates, the edge points are not weighted—they are wholly included in or excluded from the calculation, depending on the location of the grid points with respect to the specified limits. See the General Information on transformations for important details about this transformation.
Note that when @SUM is applied simultaneously to multiple axes the calculation is applied to the entire block of values rather than to the individual axes. The output will document this fact by showing "XY sum" as the transformation.
Chapter 3, Section 2.4.22
@RSUM—running unweighted sum
The transformation @RSUM computes the running unweighted sum of the variable with respect to the indicated axis. @RSUM is to @IIN as @SUM is to @DIN. The treatment of edge points is identical to @SUM. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.23
@FAV:n—averaging filler
The transformation @FAV fills holes (values flagged as invalid) in variables with the average value of the surrounding grid points along the indicated axis. The width of the averaging window is the number of points given as an argument to the transformation. The default is n=3. If an even value of n is specified, Ferret uses n+1 so that the average is centered. All of the surrounding points are weighted equally, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If any of the surrounding points are invalid they are omitted from the calculation. If all of the surrounding points are invalid the hole is not filled. See the General Information on transformations for important details about this transformation.
Example:
yes? CONTOUR/X=160W:160E/Y=5S:0 u[X=@FAV:5]
Chapter 3, Section 2.4.24
@FLN:n—linear interpolation filler
The transformation @FLN:n fills holes in variables with a linear interpolation from the nearest non-missing surrounding point. n specifies the number of points beyond the edge of the indicated axis limits to include in the search for interpolants (default n = 1). Note that this does not mean it looks only n points beyond the edges of interior gaps, but only that it looks n points beyond the limits given in the espression. Unlike @FAV, @FLN is sensitive to unevenly spaced points and computes its linear interpolation based on the world coordinate locations of grid points.
Any gap of missing values that has a valid data point on each end will be filled, regardless of the length of the gap. However, when a sub-region from the full span of the data is requested sometimes a fillable gap crosses the border of the requested region. In this case the valid data point from which interpolation should be computed is not available. The parameter n tells Ferret how far beyond the border of the requested region to look for a valid data point. See the General Information on transformations for important details about this transformation.
Example: To allow data to be filled only when gaps in i are less than 15 points, use the @CIA and @CIB transformations which return the distance from the nearest valid point.
yes? USE my_data yes? LET allowed_gap = 15 yes? LET gap_size = my_var[i=@cia] + my_var[i=@cib] yes? LET gap_mask = IF gap_size LE gap_allowed THEN 1 yes? LET my_answer = my_var[i=@fln) * gap_mask
Example: Showing the effect of the argument n
yes? let var = {1,,,,2,,,,6}
yes? list var
VARIABLE : {1,,,,2,,,,6}
SUBSET : 9 points (X)
1 / 1: 1.000
2 / 2: ....
3 / 3: ....
4 / 4: ....
5 / 5: 2.000
6 / 6: ....
7 / 7: ....
8 / 8: ....
9 / 9: 6.000
yes? ! x=3:9@fln:1 says look only one point beyond the requested limits of x=3:9 when filling
yes? list var[x=3:9@fln:1]
VARIABLE : {1,,,,2,,,,6}
linear-filled by 1 pts on X
SUBSET : 7 points (X)
3 / 3: ....
4 / 4: ....
5 / 5: 2.000
6 / 6: 3.000
7 / 7: 4.000
8 / 8: 5.000
9 / 9: 6.000
yes? ! x=3:9@fln:5 says look within 5 grid cells beyond the requested limits of x=3:9 when filling
yes? list var[x=3:9@fln:5]
VARIABLE : {1,,,,2,,,,6}
linear-filled by 5 pts on X
SUBSET : 7 points (X)
3 / 3: 1.500
4 / 4: 1.750
5 / 5: 2.000
6 / 6: 3.000
7 / 7: 4.000
8 / 8: 5.000
9 / 9: 6.000
Ch3 Sec2.4.25
@FNR—nearest neighbor filler
The transformation @FNR is similar to @FLN, except that it replicates the nearest point to the missing value. In the case of points being equally spaced around the missing point, the mean value is used. See the General Information on transformations for important details about this transformation.
If an argument is given, var[X=30:34@FNR:2] then the transformation will return data from only within that index range around the given location, here 2 index values below x=30 to 2 index values above x=34. However if the expression is given without a range of coordinates or indices to return, e.g. LET filled_var = var[X=@FNR] then any argument after @FNR will be ignored. The result will be filled with the nearest value no matter what distance it is from the missing data.
Note that as is the case with most transformations, @FNR operates in one direction at a time, so that when var[x=@FNR,y=@FNR] iks evaluated, var is filled first in X and then that result is filled in Y. The function FILL_XY will often be a better option when doing a 2-D fill operation in X and Y.
@LOC—location of
The transformation @LOC accepts an argument value—the default value is zero if no argument is specified. The transformation @LOC finds the single location at which the variable first assumes the value of the argument. The result is in units of the underlying axis. Linear interpolation is used to compute locations between grid points. If the variable does not assume the value of the argument within the specified region the @LOC transformation returns an invalid data flag. See also the discussion of @EVNT, the "event mask" transformation.
For example, temp[Z=0:200@LOC:18] finds the location along the Z axis (often depth in meters) at which the variable "temp" (often temperature) first assumes the value 18, starting at Z=0 and searching to Z=200. See the General Information on transformations for important details about this transformation.
yes? CONTOUR/X=160E:160W/Y=10S:10N temp[Z=0:200@LOC:18]
produces a map of the depth of the 18-degree isotherm. See the General Information on transformations for important details about this transformation.
Note that the transformation @LOC can be used to locate non-constant values, too, as the following example illustrates:
Example: locating non-constant values
Determine the depth of maximum salinity.
yes? LET max_salt = salt[Z=@MAX] yes? LET zero_at_max = salt - max_salt yes? LET depth_of_max = zero_at_max[Z=@LOC:0]
Chapter 3, Section 2.4.27
@WEQ—weighted equal; integration kernel
The @WEQ ("weighted equal") transformation is the subtlest and arguably the most powerful transformation within Ferret. It is a generalized version of @LOC; @LOC always determines the value of the axis coordinate (the variable X, Y, Z, or T) at the points where the gridded field has a particular value. More generally, @WEQ can be used to determine the value of any variable at those points. See also the discussion of @EVNT, the "event mask" transformation. See the General Information on transformations for important details about this transformation.
Like @LOC, the transformation @WEQ finds the location along a given axis at which the variable is equal to the given (or default) argument. For example, V1[Z=@WEQ:5] finds the Z locations at which V1 equals "5". But whereas @LOC returns a single value (the linearly interpolated axis coordinate values at the locations of equality) @WEQ returns instead a field of the same size as the original variable. For those two grid points that immediately bracket the location of the argument, @WEQ returns interpolation coefficients. For all other points it returns missing value flags. If the value is found to lie identically on top of a grid point an interpolation coefficient of 1 is returned for that point alone. The default argument value is 0.0 if no argument is specified.
Example 1
yes? LET v1 = X/4
yes? LIST/X=1:6 v1, v1[X=@WEQ:1], v1[X=@WEQ:1.2]
X: 1 to 6
Column 1: V1 is X/4
Column 2: V1[X=@WEQ:1] is X/4 (weighted equal of 1 on X)
Column 3: V1[X=@WEQ: 1.200] is X/4 (weighted equal of 1.2 on X)
V1 V1 V1
1 / 1: 0.250 .... ....
2 / 2: 0.500 .... ....
3 / 3: 0.750 .... ....
4 / 4: 1.000 1.000 0.2000
5 / 5: 1.250 .... 0.8000
6 / 6: 1.500 .... ....
The resulting field can be used as an "integrating kernel," a weighting function that when multiplied by another field and summed will give the value of that new field at the desired location.
Example 2
Using variable v1 from the previous example, suppose we wish to know the value of the function X^2 (X squared) at the location where variable v1 has the value 1.2. We can determine it as follows:
yes? LET x_squared = X^2
yes? LET integrand = x_squared * v1[X=@WEQ:1.2]
yes? LIST/X=1:6 integrand[X=@SUM] !Ferret output below
VARIABLE : X_SQUARED * V1[X=@WEQ:1.2]
X : 1 to 6 (summed)
23.20Notice that 23.20 = 0.8 * (5^2) + 0.2 * (4^2)
Below are two "real world" examples that produce fully labeled plots.
Example 3: salinity on an isotherm
Use the Levitus climatology to contour the salinity of the Pacific Ocean along the 20-degree isotherm (Figure 3_5).
yes? SET DATA levitus_climatology ! annual sub-surface climatology yes? SET REGION/X=100E:50W/Y=45S:45N ! Pacific Ocean yes? LET isotherm_20 = temp[Z=@WEQ:20] ! depth kernel for 20 degrees yes? LET integrand_20 = salt * isotherm_20 yes? SET VARIABLE/TITLE="Salinity on the 20 degree isotherm" integrand_20 yes? CONTOUR/LEV=(33,37,.2)/SIZE=0.12 integrand_20[Z=@SUM] yes? GO fland !continental fill
Example 4: month with warmest sea surface temperatures
Use the COADS data set to determine the month in which the SST is warmest across the Pacific Ocean. In this example we use the same principles as above to create an integrating kernel on the time axis. Using this kernel we determine the value of the time step index (which is also the month number, 1–12) at the time of maximum SST (Figure 3_6).
yes? SET DATA coads_climatology ! monthly surface climatology yes? SET REGION/X=100E:50W/Y=45S:45N ! Pacific Ocean yes? SET MODE CAL:MONTH yes? LET zero_at_warmest = sst - sst[l=@max] yes? LET integrand = L[G=sst] * zero_at_warmest[L=@WEQ] ! "L" is 1 to 12 yes? SET VARIABLE/TITLE="Month of warmest SST" integrand yes? SHADE/L=1:12/PAL=inverse_grayscale integrand[L=@SUM]
Example 5: values of variable at depths of a second variable:
Suppose I have V1(x,y,z) and MY_ZEES(x,y), and I want to find the values of V1 at depths MY_ZEES. The following will do that using @WEQ:
yes? LET zero_at_my_zees = Z[g=v1]-my_zees yes? LET kernel = zero_at_my_zees[Z=@WEQ:0] yes? LET integrand = kernel*v1 yes? LET v1_on_my_zees = integrand[Z=@SUM]
Chapter 3, Section 2.4.28
@ITP—interpolate
The @ITP transformation provides the same linear interpolation calculation that is turned on modally with SET MODE INTERPOLATE but with a higher level of control, as @ITP can be applied selectively to each axis. @ITP may be applied only to point locations along an axis. The result is the linear interpolation based on the adjoining values. Interpolation can be applied on an axis by axis and variable by variable basis like any other transformation. To apply interpolation use the transformation "@ITP" in the same way as, say, @SBX, specifying the desired location to which to interpolate. For example, on a Z axis with grid points at Z=10and Z=20 the syntax my_var[Z=14@ITP] would interpolate to Z=14 with the computation
0.6*my_var[Z=10]+0.4*my_var[Z=20].
The example which follows illustrates the interpolation control that is possible using @ITP:
! with modal interpolation
yes? SET DATA coads_climatology
yes? SET MODE INTERPOLATE
yes? LIST/L=1/X=180/Y=0 sst ! interpolates both lat and long
VARIABLE : SEA SURFACE TEMPERATURE (Deg C)
FILENAME : coads_climatology.cdf
FILEPATH : /home/porter/tmap/ferret/linux/fer_dsets/data/
LONGITUDE: 180E (interpolated)
LATITUDE : 0 (interpolated)
TIME : 16-JAN 06:00
28.36
! with no interpolation
yes? CANCEL MODE INTERPOLATE
yes? LIST/L=1/X=180/Y=0 sst ! gives value at 179E, 1S
VARIABLE : SEA SURFACE TEMPERATURE (Deg C)
FILENAME : coads_climatology.cdf
FILEPATH : /home/porter/tmap/ferret/linux/fer_dsets/data/
LONGITUDE: 179E
LATITUDE : 1S
TIME : 16-JAN 06:00
28.20
! using @ITP to interpolate in longitude, only
yes? LIST/L=1/Y=0 sst[X=180@ITP] ! latitude remains 1S
VARIABLE : SEA SURFACE TEMPERATURE (Deg C)
FILENAME : coads_climatology.cdf
FILEPATH : /home/porter/tmap/ferret/linux/fer_dsets/data/
LONGITUDE: 180E (interpolated)
LATITUDE : 1S
TIME : 16-JAN 06:00
28.53
See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.29
Syntax options:
|
@CDA |
Distance to closest valid point above each point along the indicated axis |
|
@CDA:n |
Closest distance to a valid point above the indicated points, searching only within n points |
The transformation @CDA will compute at each grid point how far it is to the closest valid point above this coordinate position on the indicated axis. The optional argument n gives a maximum distance to search for valid data. N is in integer units: how far to search forward in index space. The distance will be reported in the units of the axis. If a given grid point is valid (not missing) then the result of @CDA for that point will be 0.0. See the example for @CDB below. The result's units are now axis units, e.g., degrees of longitude to the next valid point above. See the General Information on transformations for important details about this transformation, and see the example under @CDB below.
Chapter 3, Section 2.4.30
Syntax options:
|
@CDB |
Distance to closest valid point below each point along the indicated axis |
|
@CDB:n |
Closest distance to a valid point below the indicated points, searching only within n points |
The transformation @CDB will compute at each grid point how far it is to the closest valid point below this coordinate position on the indicated axis. The optional argument n gives a maximum distance to search for valid data. N is in integer units: how far to search backward in index space. The distance will be reported in the units of the axis. The distance will be reported in the units of the axis. If a given grid point is valid (not missing) then the result of @CDB for that point will be 0.0. The result's units are now axis units, e.g., degrees of longitude to the next valid point below. See the General Information on transformations for important details about this transformation.
Example:
yes? USE coads_climatology
yes? SET REGION/x=125w:109w/y=55s/l=1
yes? LIST sst, sst[x=@cda], sst[x=@cdb] ! results below
Column 1: SST is SEA SURFACE TEMPERATURE (Deg C)
Column 2: SST[X=@CDA:1] is SEA SURFACE TEMPERATURE (Deg C)(closest dist above on X)
Column 3: SST[X=@CDB:1] is SEA SURFACE TEMPERATURE (Deg C)(closest dist below on X)
SST SST SST
125W / 108: 6.700 0.000 0.000
123W / 109: .... 8.000 2.000
121W / 110: .... 6.000 4.000
119W / 111: .... 4.000 6.000
117W / 112: .... 2.000 8.000
115W / 113: 7.800 0.000 0.000
113W / 114: 7.800 0.000 0.000
111W / 115: .... 2.000 2.000
109W / 116: 8.300 0.000 0.000
yes? list sst[x=121w], sst[x=121w@cda:2], sst[x=121w@cda:5], sst[x=121w@cdb:5]
Chapter 3, Section 2.4.31
@CIA—closest index above
Syntax options:
|
@CIA |
Index of closest valid point above each point along the indicated axis |
|
@CIA:n |
Closest distance in index space to a valid point above the point at index or coordinate m, searching only within n points |
The transformation @CIA will compute at each grid point how far it is to the closest valid point above this coordinate position on the indicated axis. The optional argument n gives a maximum distance to search from the index or coordinate location m for valid data. N is in integer units: how far to search forward in index space. The distance will be reported in terms of the number of points (distance in index space). If a given grid point is valid (not missing) then the result of @CIA for that point will be 0.0. See the example for @CIB below. The units of the result are grid indices; integer number of grid units to the next valid point above. See the General Information on transformations for important details about this transformation, and see the example under @CIB below.
Chapter 3, Section 2.4.32
@CIB—closest index below
Syntax options:
|
@CIB |
Index of closest valid point below each point along the indicated axis |
|
@CIB:n |
Closest distance in index space to a valid point below the indicated points, searching only within n points |
The transformation @CIB will compute at each grid point how far it is to the closest valid point below this coordinate position on the indicated axis. The optional argument n gives a maximum distance to search for valid data. N is in integer units: how far to search backward in index space. The distance will be reported in terms of the number of points (distance in index space). If a given grid point is valid (not missing) then the result of @CIB for that point will be 0.0. The units of the result are grid indices, integer number of grid units to the next valid point below. See the General Information on transformations for important details about this transformation.
Example:
yes? USE coads_climatology yes? SET REGION/x=125w:109w/y=55s/l=1 yes? LIST sst, sst[x=@cia], sst[x=@cib] ! results below Column 1: SST is SEA SURFACE TEMPERATURE (Deg C) Column 2: SST[X=@CIA:1] is SEA SURFACE TEMPERATURE (Deg C) (closest dist above on X ...) Column 3: SST[X=@CIB:1] is SEA SURFACE TEMPERATURE (Deg C) (closest dist below on X ...) SST SST SST 125W / 108: 6.700 0.000 0.000 123W / 109: .... 4.000 1.000 121W / 110: .... 3.000 2.000 119W / 111: .... 2.000 3.000 117W / 112: .... 1.000 4.000 115W / 113: 7.800 0.000 0.000 113W / 114: 7.800 0.000 0.000 111W / 115: .... 1.000 1.000 109W / 116: 8.300 0.000 0.000 yes? list sst[x=121w], sst[x=121w@cia:2], sst[x=121w@cia:5], \ sst[x=121w@cib:5] DATA SET: /home/ja9/tmap/fer_dsets/data/coads_climatology.cdf LONGITUDE: 121W LATITUDE: 55S TIME: 16-JAN 06:00 Column 1: SST is SEA SURFACE TEMPERATURE (Deg C) Column 2: SST[X=@CIA:2] is SEA SURFACE TEMPERATURE (Deg C) Column 3: SST[X=@CIA:5] is SEA SURFACE TEMPERATURE (Deg C) Column 4: SST[X=@CIB:5] is SEA SURFACE TEMPERATURE (Deg C) SST SST SST SST
I / *: .... .... 3.000 2.00
This transformation locates "events" in data. An event is the occurrence of a particular value. The output steps up by a value of 1 for each event, starting from a value of zero. (If the variable takes on exactly the value of the event trigger the +1 step occurs on that point. If it crosses the value, either ascending or descending, the step occurs on the first point after the crossing.)
For example, if you wanted to know the maximum value of the second wave, where (say) rising above a magnitude of 0.1 in variable "ht" represented the onset of a wave, then
yes? LET wave2_mask = IF ht[T=@evnt:0.1] EQ 2 THEN 1
is a mask for the second wave, only. The maximum waveheight may be found with
yes? LET wave2_ht = wave2_mask * ht yes? LET wave2_max_ht = wave2_ht[T=@max]
Note that @EVNT can be used together with @LOC and @WEQ to determine the location when an event occurs and the value of other variables as the event occurs, respectively. Since there may be missing values in the data, and since the instant at which the event occurs may lie immediately before the step in value for the event mask, the following expression is a general solution.
yes? LET event_mask = my_var[t=@evnt:<value>] yes? LET event_n = IF ABS(MISSING(event_mask[L=@SBX],event_mask)-n) LE 0.67 THEN my_var
So that
event_n[t=@LOC:<value>]
is the time at which event "n" occurs, and
event_n[t=@WEQ:<value>]
is the integrating kernel (see @WEQ). See the General Information on transformations for important details about this transformation.
@MED—median transform smoother
Syntax:
|
@MED:n |
Replace each value with its median based on the surrounding n points, where n must be odd. |
The transformation @MED applies a median window, replacing each value with its median, to smooth the variable along the indicated axis. The width of the median window is the number of points given as an argument to the transformation. The default width is 3 points. No weighting is applied, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If there is missing data within the window, the median is based on the points that are present. See the General Information on transformations for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0 u[L=1:120@MED:5]
The transformation @MED does not reduce the number of points along the axis; it replaces each of the original values with the median of its surrounding points. Regridding can be used to reduce the number of points.
Chapter 3, Section 2.4.34
@SMN - Smoothing with minimum
Syntax:
SMN:n
Replace each value with its minimum based on the surrounding n points, where n must be odd.
The transformation @SMN applies a minimum window, replacing each value with its minimum, to smooth the variable along the indicated axis. The width of the minimum window is the number of points given as an argument to the transformation. The default width is 3 points. No weighting is applied, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If there is missing data within the window, the minimum is based on the points that are present. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.35
@SMX - Smoothing with maximum
Syntax :
|
SMX:n |
Replace each value with its maximum based on the surrounding n points, where n must be odd. |
The transformation @SMX applies a maximum window, replacing each value with its maximum, to smooth the variable along the indicated axis. The width of the maximum window is the number of points given as an argument to the transformation. The default width is 3 points. No weighting is applied, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If there is missing data within the window, the maximum is based on the points that are present. See the General Information on transformations for important details about this transformation.
Chapter 3, Section 2.4.36
@WGT - return weights
Syntax:
|
@WGT |
Replace each value with the weights used in an averaging or integral on the same grid. |
The transformation @WGT returns the weights used in an equivalent transformation averaging or integrating on the same grid. The results are expressed in the same standard units as integrals: Meters for degrees longitude or latitude on the surface of the earth and seconds in time; for axes with other units the results are in the units of the axis. See the General Information on transformations for important details about this transformation.
Example:
yes? use levitus_climatology
yes? list/y=0/x=140w/z=0:90 temp[z=@wgt]
VARIABLE : TEMPERATURE (DEG C)
weights for avg,int on Z
FILENAME : levitus_climatology.cdf
FILEPATH : /home/users/tmap/ferret/linux/fer_dsets/data/
SUBSET : 7 points (DEPTH (m))
LONGITUDE: 140.5W
LATITUDE : 0.5S
140.5W
200
0 / 1: 5.00
10 / 2: 10.00
20 / 3: 10.00
30 / 4: 15.00
50 / 5: 22.50
75 / 6: 25.00
100 / 7: 2.50
Ch3 Sec2.5. IF-THEN logic ("masking") and IFV-THEN
Ferret expressions can contain embedded IF-THEN-ELSE logic. The syntax of the IF-THEN logic is simply (by example)
LET a = IF a1 GT b THEN a1 ELSE a2 or LET a = IFV a1 GT b then a1 ELSE a2
(read as "if a1 is greater than b then a1 else a2").
The IFV syntax differs from IF in that the result of the IF is false wherever the value is missing or if it is zero. IFV returns false only if the value is missing - valid zero values are treated as true. All of the syntax for IF in this section is also valid using IFV. IFV was introduced with Ferret version 6.71. Note that there is no IFV syntax for conditional execution. There is a further example using IFV at the end of this section.
This syntax is especially useful in creating masks that can be used to perform calculations over regions of arbitrary shape. For example, we can compute the average air-sea temperature difference in regions of high wind speed using this logic:
SET DATA coads_climatology SET REGION/X=100W:0/Y=0:80N/T=15-JAN LET fast_wind = IF wspd GT 10 THEN 1 LET tdiff = airt - sst LET fast_tdiff = tdiff * fast_wind
When defining a mask, if no ELSE statement is used, there is an implied "ELSE bad-value".
We can also make compound IF-THEN statements. The parentheses are included here for clarity, but are not necessary.
LET a = IF (b GT c AND b LT d) THEN e LET a = IF (b GT c OR b LT d) THEN e LET a = IF (b GT c AND b LT d) THEN e ELSE q
The user may find it clearer to think of this logic as WHERE-THEN-ELSE to avoid confusion with the IF used to control conditional execution of commands. Again, if there is no ELSE, there is an implied "ELSE bad-value". Compound and multi-line IF-THEN-ELSE constructs are not allowed in embedded logic.
Note that if the data contains values that are exactly Zero, then "IF var" (comparison to the missing-flag for the variable) will be false when the data is missing and ALSO when its value is zero. This is because Ferret does not have a logical data type, and so zero is equivalent to FALSE. See the documentation on the IF syntax. To handle this case, you can use the IFV keyword, or with classic "IF", get the missing-value for the variable and use it to define the expression.
yes? LET mask = IF var NE `var,RETURN=bad` THEN 1 or yes? LET mask = IFV var THEN 1
Example demonstrating IFV: Define and plot a variable that has integer values: 0, 1,... 6. Notice the missing data in the southern ocean. A mask using IF will mask out all the zero values, whereas a mask with IFV treats those zero's as valid.
! Define the variable with values 0 through 6. yes? USE coads_climatology; SET REG/L=1 yes? LET intvar = INT(sst/5) ! Define a mask using this variable and IF yes? LET mask = IF intvar THEN 1 ! Define a mask using this variable yes? LET maskV = IFV intvar THEN 1 yes? set view ul; shade/title="Variable with a few integer values"/lev=(0,6,1) intvar yes? go land yes? set view ll; shade/title="Mask with classic IF: IF var then 1" mask yes? go land yes? set view lr yes? shade/title="Mask with ifValid IFV: IFV var then 1" maskV yes? go land
Lists of constants ("constant arrays")
The syntax {val1, val2, val3} is a quick way to enter a list of constants. For example
yes? LIST {1,3,5}, {1,,5}
X: 0.5 to 3.5
Column 1: {1,3,5}
Column 2: {1,,5}
{1,3,5} {1,,5}
1 / 1: 1.000 1.000
2 / 2: 3.000 ....
3 / 3: 5.000 5.000Note that a constant variable is always an array oriented in the X direction To create a constant aray oriented in, say, the Y direction use YSEQUENCE
yes? STAT/BRIEF YSEQUENCE({1,3,5})
Total # of data points: 3 (1*3*1*1)
# flagged as bad data: 0
Minimum value: 1
Maximum value: 5
Mean value: 3 (unweighted average)Below are two examples illustrating uses of constant arrays. Try running the the constant_array_demo journal script.
Ex. 1) plot a triangle (Figure 3_7)
LET xtriangle = {0,.5,1}
LET ytriangle = {0,1,0}
POLYGON/LINE=8 xtriangle, ytriangle, 0
Or multiple triangles (Figure 3_8) See polymark.jnl regarding this figure
Ex. 2) Sample Jan, June, and December from sst in coads_climatology
yes? USE coads_climatology
yes? LET my_sst_months = SAMPLEL(sst, {1,6,12})
yes? STAT/BRIEF my_sst_months
Total # of data points: 48600 (180*90*1*3)
# flagged as bad data: 21831
Minimum value: -2.6
Maximum value: 31.637
Mean value: 17.571 (unweighted average)